Question

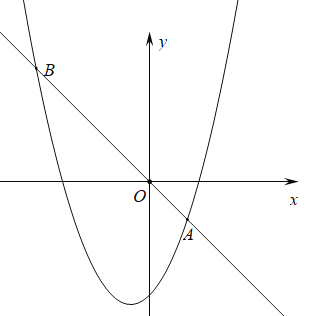
【题目】如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，与函数的图象的一个交点为．

（1）求，，的值；

（2）将线段向右平移得到对应线段，当点落在函数的图象上时，求线段扫过的面积．

Answer 1

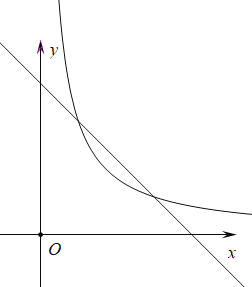
【答案】（1）m=4, n=1,k=3.（2）3.

【解析】

（1） 把点，分别代入直线中即可求出m=4，再把代入直线即可求出n=1.把代入函数求出k即可；

（2）由（1）可求出点B的坐标为（0，4），点B‘是由点B向右平移得到，故点B’的纵坐标为4，把它代入反比例函数解析式即可求出它的横坐标，根据平移的知识可知四边形AA’B’B是平行四边形，再根据平行四边形的面积计算公式计算即可.

解：（1）把点，分别代入直线中得：

-4+m=0,

m=4,

∴直线解析式为.

把代入得：

n=-3+4=1.

∴点C的坐标为（3，1）

把（3，1）代入函数得：

解得：k=3.

∴m=4, n=1,k=3.

(2)如图，设点B的坐标为（0，y）则y=-0+4=4

∴点B的坐标是（0，4）

当y=4时，

解得，

∴点B’（ ，4）

∵A’,B’是由A,B向右平移得到，

∴四边形AA’B’B是平行四边形，

故四边形AA’B’B的面积=4=3.