题目内容
【题目】某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第![]() 天生产的防护服数量为
天生产的防护服数量为![]() 件,
件,![]() 与
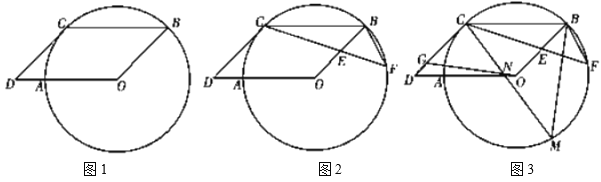
与![]() 之间的关系可以用图中的函数图象来刻画.
之间的关系可以用图中的函数图象来刻画.

(1)直接写出![]() 与
与![]() 的函数关系式________;
的函数关系式________;
(2)由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第![]() 天创造的利润为
天创造的利润为![]() 元,直接利用(1)的结论,求
元,直接利用(1)的结论,求![]() 与
与![]() 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
【答案】(1)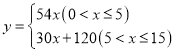 ,
,![]() 为正整数;(2)
为正整数;(2)![]() ,
,![]() ,第8天的利润最大,最大利润是8640元
,第8天的利润最大,最大利润是8640元
【解析】
(1)根据图像分别写出当0<x≤5和5<x≤15时的函数即可;(2)设每件防护服的成本为![]() 元.(2)设每件防护服的成本为
元.(2)设每件防护服的成本为![]() 元,分别写出当0<x≤5和5<x≤15时求出最大利润,在进行比较即可
元,分别写出当0<x≤5和5<x≤15时求出最大利润,在进行比较即可
解:(1)当0<x≤5时,设表达式为y=kx
由题意得:270=5k,解得k=54
所以解析式为y=54x
当5<x≤15时,设表达式为y=kx+b
由题意得: ![]() ,解得
,解得![]()
所以解析式为y=30x+120
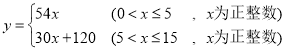
(2)设每件防护服的成本为![]() 元,①当
元,①当![]() 时,
时,![]() ,则利润
,则利润![]()
∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() (元)
(元)
②![]() 时,
时,![]() ,则利润
,则利润![]()
![]()
![]()
![]()
∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() (元)
(元)
综上所述,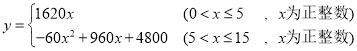
第8天的利润最大,最大利润是多少元8640元.

练习册系列答案
相关题目
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3