题目内容
已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
(1)k≤(3分); (2)k=-3(5分 【解析】试题分析:(1)方程有两个实数根,可得△=b2﹣4ac≥0,代入可解出k的取值范围; (2)结合(1)中k的取值范围,由题意可知,x1+x2=2(k﹣1)<0,去绝对值号结合等式关系,可得出k的值. 【解析】 (1)由方程有两个实数根,可得 △=b2﹣4ac=4(k﹣1)2﹣4k2=4k2﹣8k+4﹣4k2=﹣8k...
练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目


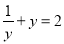
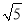 ,BC=4
,BC=4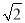 ,DE=3.
,DE=3.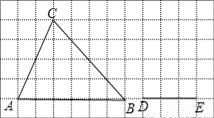
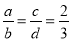 ,则
,则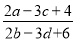 的值为_________.
的值为_________.