题目内容
已知点 和点
和点 在抛物线
在抛物线 上.
上.
( 1)求
1)求 的值及点
的值及点 的坐标;
的坐标;
(2)点 在
在 轴上,且满足△
轴上,且满足△ 是以
是以 为直角边的直角三角形,求点
为直角边的直角三角形,求点 的坐标;
的坐标;
(3)平移抛物线 ,记平移后点A的对应点为
,记平移后点A的对应点为 ,点B的对应点为
,点B的对应点为 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时, 最短,求此时抛物线的函数解析式
最短,求此时抛物线的函数解析式
 |
解:(1)
抛物线解析式为:

 (2) 记直线AB与x、y轴分别交于C、D两点,
(2) 记直线AB与x、y轴分别交于C、D两点,



①以A为直角顶点,则

则

又

②以 为直角顶点,则
为直角顶点,则





(3)记点A关于x轴的对称点为
则BE: 
令y=0,得
即BE与x轴的交点为

故抛物线 向右平移
向右平移 个单位时
个单位时 最短
最短
此时,抛物线的解析式为

练习册系列答案
相关题目
 先沿
先沿 轴向右平移1个单位, 再沿
轴向右平移1个单位, 再沿 轴向上移2个单位,所得抛物线的解析式是
轴向上移2个单位,所得抛物线的解析式是 B.
B.
 D.
D.

 )
)
 ,在正三角形中,我们可推得:
,在正三角形中,我们可推得: ;在正方形中,可推得:
;在正方形中,可推得: ;在正五边形中,可推得:
;在正五边形中,可推得: ,依此类推在正八边形中,
,依此类推在正八边形中,
 ,在正
,在正 边形中,
边形中,
 中,
中, ,
, 于
于 ,
, ,若
,若 ,
, ,求
,求 的值及CD的长.
的值及CD的长.
 中,点
中,点 分别在
分别在 边上,
边上, ∥
∥ ,若
,若 ,
, ,则
,则 等于
等于
 B.
B.  C.
C.  D.
D. 

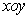 中,直线
中,直线 和抛物线
和抛物线 在第一象限交于点A, 过A作
在第一象限交于点A, 过A作 轴于点
轴于点 .如果
.如果 取1,2,3,…,n时对
取1,2,3,…,n时对 应的△
应的△ 的面积为
的面积为
 ,那么
,那么 _____;
_____; _____.
_____.
 B.
B. C.
C. D.
D.

 角
角 、
、 分别为30°和60°,点F、E、C在同一直线上.
分别为30°和60°,点F、E、C在同一直线上. )
)