题目内容
1、点M（x、y）的坐标满足|x+y|＜|x-y|，则点M所在象限为（ ）
分析：根据点M（x、y）的坐标满足|x+y|＜|x-y|，两边平方可消去x2+y2，剩余xy的形式，判断出x、y的符号关系，进而确定出点M（x，y）所在的象限．
解答：解：∵|x+y|＜|x-y|
∴两边平方得（x+y）2＜（x-y）2?x2+2xy+y2＜x2-2xy+y2?xy＜0
则点M（x，y）在2、4象限．
故答案为B
∴两边平方得（x+y）2＜（x-y）2?x2+2xy+y2＜x2-2xy+y2?xy＜0
则点M（x，y）在2、4象限．
故答案为B
点评：本题考查完全平方式、点的坐标．解决本题的关键是利用完全平方式，判断出x、y的符号关系，进而确定所在象限．
练习册系列答案
相关题目
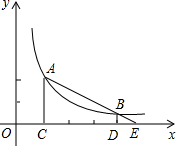如图，A、B是反比例函数
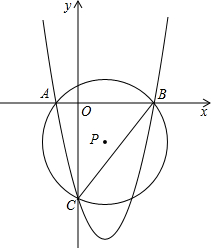已知抛物线y=x2+bx+c与y轴交于点C，与x轴交于点A（-1，0）、B（4，0），