题目内容
6.式子$\frac{{x}^{2}-x-2}{\sqrt{1-x}}$值为0时,x=-1.分析 利用分式值为0的条件和二次根式有意义的条件求解即可.
解答 解:∵$\frac{{x}^{2}-x-2}{\sqrt{1-x}}$值为0,
∴x2-x-2=0且1-x>0,
解得:x=2或x=-1,且x<1,
∴x=-1,
故答案为:-1.
点评 本题主要考查了分式值为0和二次根式的意义及分式的意义,注意分母不为0是解答此题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
17.在式子:①(x-1)0,②$\sqrt{x-1}$,③$\frac{1}{x-1}$中,x可以取1的是( )
| A. | ①和② | B. | 只有① | C. | 只有② | D. | 只有③ |
16.在平面直角坐标系中.点P(1,-2)关于y轴的对称点的坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (-1,2) | D. | (-2,1) |
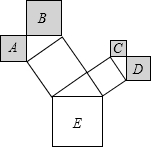 如图是一棵勾股树,它是由正方形和直角三角形拼成的额,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
如图是一棵勾股树,它是由正方形和直角三角形拼成的额,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( ) 如图,两条直线a,b相交于O,若∠α=60°,则∠β=120°.
如图,两条直线a,b相交于O,若∠α=60°,则∠β=120°.


