题目内容
13.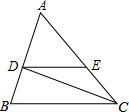 已知,如图,△ABC中,CD平分∠ACB,DE∥BC,AD:DB=7:5,AC=24,求DE的长.
已知,如图,△ABC中,CD平分∠ACB,DE∥BC,AD:DB=7:5,AC=24,求DE的长.
分析 根据平行线分线段成比例的知识求出AE,EC,然后判断ED=EC,即可得出答案.
解答 解:∵DE∥BC,
∴$\frac{AD}{DB}=\frac{AE}{EC}=\frac{7}{5}$,
又∵AC=24,
∴AE=14,EC=10,
∵CD平分∠ACB交AB于D,
∴∠ACD=∠DCB,
又∵DE∥BC,
∴∠EDC=∠DCB,
∴∠ACD=∠EDC,
∴DE=EC=10.
点评 本题考查了相似三角形的判定与性质,解答本题的关键是掌握平行线的性质及相似三角形的性质:对应边成比例,难度一般.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
3.一个不透明的袋子中装有4个红球,2个黄球,这些球除了颜色外都相同,从中随机抽出3个球,下列事件为必然事件的是( )
| A. | 至少有1个球是红球 | B. | 至少有1个球是黄球 | ||
| C. | 至少有2个球是红球 | D. | 至少有2个球是黄球 |
4.若多项式4x2+mx+1是完全平方式,则m的值是( )
| A. | ±4 | B. | 4 | C. | ±2 | D. | 2 |
1.下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
| A. | a=$\sqrt{5}$ b=2 c=3 | B. | a=7 b=24 c=5 | C. | a=6 b=8 c=10 | D. | a=3 b=4 c=5 |
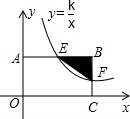 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=1,则k的值为4.
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=1,则k的值为4.
 如图,一艘客轮在大平洋中航行,所在位置是A(140°,20°),10小时后到达B地,用坐标表示B地的位置是(120°,30°).
如图,一艘客轮在大平洋中航行,所在位置是A(140°,20°),10小时后到达B地,用坐标表示B地的位置是(120°,30°).