题目内容
18.已知反比例函数y=$\frac{k}{x}$(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x值的增大而增大,那么这个反比例函数的表达式可以是y=-$\frac{2}{x}$.(写出一个即可)分析 首先根据反比例函数的性质可得k<0,再写一个符合条件的数即可.
解答 解:∵反比例函数y=$\frac{k}{x}$(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,
∴k<0,
∴y=-$\frac{2}{x}$.
故答案为:y=-$\frac{2}{x}$.
点评 此题主要考查了反比例函数的性质,关键是掌握对于反比例函数y=$\frac{k}{x}$,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大

练习册系列答案
相关题目
3.关于x的一元二次方程(a-2)x2+x+a2=0的一个根是0,则a的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 0 |
7.若 表示运算x+z-(y+w),则
表示运算x+z-(y+w),则 的结果是( )
的结果是( )
 表示运算x+z-(y+w),则
表示运算x+z-(y+w),则 的结果是( )
的结果是( )| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
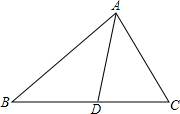 如图所示,AD为△ABC的角平分线,AB=5,AC=4,△ABD和△ABC的面积分别为S△ABD和S△ABC,那么S△ABD:S△ABC=5:9.
如图所示,AD为△ABC的角平分线,AB=5,AC=4,△ABD和△ABC的面积分别为S△ABD和S△ABC,那么S△ABD:S△ABC=5:9. 如图,在△ABC中,AD为中线,点E在AB上,连接ED并延长,与∠DAC的平分线AF交于点F.
如图,在△ABC中,AD为中线,点E在AB上,连接ED并延长,与∠DAC的平分线AF交于点F.