题目内容
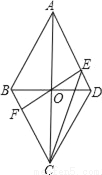
如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是( )
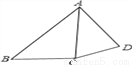
A. AB﹣AD>CB﹣CD B. AB﹣AD=CB﹣CD
C. AB﹣AD<CB﹣CD D. AB﹣AD与CB﹣CD的大小关系不确定
A 【解析】如图,在AB上截取AE=AD,连接CE. ∵AC平分∠BAD, ∴∠BAC=∠DAC, 又AC是公共边, ∴△AEC≌△ADC(SAS), ∴AE=AD,CE=CD, ∴AB-AD=AB-AE=BE,BC-CD=BC-CE, ∵在△BCE中,BE>BC-CE, ∴AB-AD>CB-CD. 故选A.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 | 实践能力 | 成长记录 | |
甲 | 90 | 83 | 95 |
乙 | 88 | 90 | 95 |
丙 | 90 | 88 | 90 |
A. 甲 B. 乙、丙 C. 甲、乙 D. 甲、丙
C 【解析】由题意知,甲的总评成绩=90×50%+83×20%+95×30%=90.1, 乙的总评成绩=88×50%+90×20%+95×30%=90.5, 丙的总评成绩=90×50%+88×20%+90×30%=89.6, ∴甲、乙的学期总评成绩是优秀. 故选C.

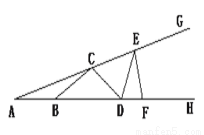
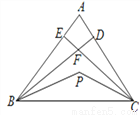
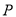 为
为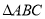 内一点,
内一点, 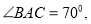
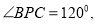
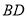 是
是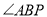 的平分线,
的平分线, 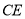 是
是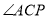 的平分线,
的平分线, 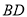 与
与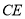 交于
交于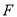 ,则
,则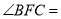 ( )
( )
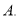
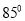
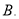
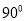
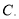
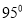
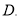

 小时,
小时,