题目内容
已知：如图，在平行四边形ABCD中，E是边AB的中点，点F在边BC上，且CF=3BF，EF与BD相交于点G．则BG：DG=________．
1：5
分析：过点E作EO∥AD交BD于O点，根据平行线分线段成比例定理得到点O为BD的中点，EO=
AD，又CF=3BF，得OE=2BF，易证得△BFG∽△OEG，得BG：GO=BF：OE=1：2，即可得到BG：DG．
解答：过点E作EO∥AD交BD于O点，如图，
∵E是边AB的中点，
∴点O为BD的中点，EO=AD，
∵四边形ABCD为平行四边形，
∴AD=BC，
又∵CF=3BF，
∴OE=2BF，
∵OE∥BF，
∴△BFG∽△OEG，
∴BG：GO=BF：OE=1：2，
而OD=OB，
∴BG：DG=1：5．
故答案为1：5．
点评：本题考查了三角形相似的判定与性质：如果两个三角形两组对应角相等，那么这两个三角形相似；相似三角形的对应边的比相等．也考查了平行四边形的性质．
分析：过点E作EO∥AD交BD于O点，根据平行线分线段成比例定理得到点O为BD的中点，EO=
AD，又CF=3BF，得OE=2BF，易证得△BFG∽△OEG，得BG：GO=BF：OE=1：2，即可得到BG：DG．解答：过点E作EO∥AD交BD于O点，如图，
∵E是边AB的中点，
∴点O为BD的中点，EO=
AD，∵四边形ABCD为平行四边形，
∴AD=BC，
又∵CF=3BF，
∴OE=2BF，
∵OE∥BF，
∴△BFG∽△OEG，
∴BG：GO=BF：OE=1：2，
而OD=OB，
∴BG：DG=1：5．
故答案为1：5．
点评：本题考查了三角形相似的判定与性质：如果两个三角形两组对应角相等，那么这两个三角形相似；相似三角形的对应边的比相等．也考查了平行四边形的性质．
练习册系列答案
名校课堂系列答案
相关题目
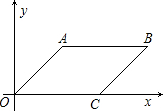如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，