题目内容
如图，在等边△ABC中，D、E分别是AB、AC的中点，DE=3，则△ABC的周长是
- A.6
- B.9
- C.18
- D.24
C
分析：根据三角形的中位线定理，即可求得等边三角形的一边长，再根据等边三角形的三边相等求得其周长．
解答：∵D、E分别是AB、AC的中点，
∴DE是△ABC的中位线，
∵DE=3，
∴BC=2DE=2×3=6，
在等边△ABC中，AB=BC=CA，
∴△ABC的周长=AB+BC+AC=3BC=3×6=18．
故选C．
点评：本题考查了三角形中位线的性质和等边三角形的性质，比较简单．
分析：根据三角形的中位线定理，即可求得等边三角形的一边长，再根据等边三角形的三边相等求得其周长．
解答：∵D、E分别是AB、AC的中点，
∴DE是△ABC的中位线，
∵DE=3，
∴BC=2DE=2×3=6，
在等边△ABC中，AB=BC=CA，
∴△ABC的周长=AB+BC+AC=3BC=3×6=18．
故选C．
点评：本题考查了三角形中位线的性质和等边三角形的性质，比较简单．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
16、如图，在等边△ABC的边BC上任取一点D，作∠ADE=60°，DE交∠C的外角平分线于E，则△ADE是
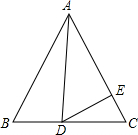如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的面积为（ ）A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
21、如图，在等边△ABC中，AD是∠BAC的平分线，点E在AC边上，且∠EDC=15°．
如图，在等边△ABC中，D是AC的中点，延长BC到点E，使CE=CD，AB=10cm．
如图，在等边△ABC中，BF是高，D是BF上一点，且OF=AF，作OE⊥BF，垂足为D，且OE=OB，连AE、AO、BE，求证：