题目内容
4.如果一个直角三角形的两条直角边长分别为5cm、12cm,另一个与其相似的直角三角形的斜边长为20cm,求另一个直角三角形斜边上的高.分析 根据勾股定理和三角形的面积公式求出这个三角形斜边上的高,根据相似三角形的性质列出比例式计算即可.
解答 解:∵一个直角三角形的两条直角边长分别为5cm、12cm,
由勾股定理得,斜边=$\sqrt{{5}^{2}+1{2}^{2}}$=13cm,
设斜边上的高为h,
则$\frac{1}{2}$×5×12=$\frac{1}{2}$×13×h,
解得,h=$\frac{60}{13}$,
设另一个直角三角形斜边上的高为n,
由题意得,$\frac{13}{20}$=$\frac{\frac{60}{13}}{n}$,
解得,n=$\frac{1200}{169}$,
答:另一个直角三角形斜边上的高为$\frac{1200}{169}$.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应高的比等于相似比是解题的关键,注意勾股定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
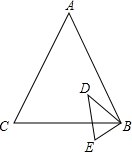 如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$.
如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$. 如图,AB,CD相交于点O,AC∥BD,已知DB:AC=3:5,△DBO的面积为18cm2,求△CAO的面积.
如图,AB,CD相交于点O,AC∥BD,已知DB:AC=3:5,△DBO的面积为18cm2,求△CAO的面积. 如图,已知等腰△ABC中,腰AB=8c,DE是腰AC的垂直平分线,垂足为点D,与AB相交于点E,△BCE的周长为14cm,求BC的长.
如图,已知等腰△ABC中,腰AB=8c,DE是腰AC的垂直平分线,垂足为点D,与AB相交于点E,△BCE的周长为14cm,求BC的长.