题目内容
如图,△ABC的内切圆分别切 、
、 、
、 于D、E、F三点,其中P、Q两点分别在
于D、E、F三点,其中P、Q两点分别在 、
、 上.若∠A=30°,∠B=80°,∠C=70°,则弧长
上.若∠A=30°,∠B=80°,∠C=70°,则弧长 与弧长
与弧长 的比值为( )
的比值为( )
A.

B.

C.

D.

【答案】分析:设△ABC的内切圆的圆心为O,连接OD、OE、OF,所以∠ADO=∠AFO=∠BDO=∠BEO=90°;再根据四边开的内角和定理,∠A+∠DOF=180°,则∠ADO=150°,同理∠EOD=180°-80°=100°;最后由弧的比等于弧所对的圆心角的比,可得出弧长 与弧长
与弧长 的比值2:3.
的比值2:3.
解答: 解:设△ABC的内切圆的圆心为O,连接OD、OE、OF,
解:设△ABC的内切圆的圆心为O,连接OD、OE、OF,
∵∠ADO=∠AFO=∠BDO=∠BEO=90°,
∴∠A+∠DOF=180°,
∴∠DOF=150°,
同理∠EOD=180°-80°=100°,
∴弧长 与弧长
与弧长 的比值2:3.
的比值2:3.
故选A.
点评:本题主要考查了内切圆的性质及弧长的比.
 与弧长
与弧长 的比值2:3.
的比值2:3.解答:
 解:设△ABC的内切圆的圆心为O,连接OD、OE、OF,
解:设△ABC的内切圆的圆心为O,连接OD、OE、OF,∵∠ADO=∠AFO=∠BDO=∠BEO=90°,
∴∠A+∠DOF=180°,
∴∠DOF=150°,
同理∠EOD=180°-80°=100°,
∴弧长
 与弧长
与弧长 的比值2:3.
的比值2:3.故选A.
点评:本题主要考查了内切圆的性质及弧长的比.

练习册系列答案
相关题目
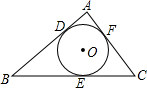 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.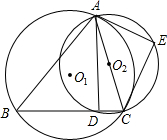 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3
