题目内容
设a,b都是正整数,若二次函数y=a2+bx+1的图象与x轴有两个交点,且这两个交点的横坐标x1,x2,满足-1<x1<x2<0,
求:正整数a,b的最小值及此时x1,x2的值.
解:解法1:依题意,x1,x2为方程ax2+bx+1=0的两实根,
则b2-4a>0①
x1+x2= ,x1x2=
,x1x2= ②,
②,
∵-1<x1<x2<0,
∴1+x1>0,1+x2>0,
即(1+x1)(1+x2)>0,
∴(1+x1)(1+x2)=1+x1+x2+x1x2=1- =
= >0,
>0,
而a>0,
∴a-b+1>0,即:a>b+1,又a,b都是正整数,则a≥b③,
由①得,b>2 ④,
④,
由③、④得a>2 ,即
,即 >2,
>2,
∴a>4,因此正整数a的最小值为5.
由④得:b>2 >4,
>4,
∴正整数b的最小值为5,
当a=b=5时,ax2+bx+1=0的根为x= ,
,
∴ ,
,
解法2:依题意:y=ax2+bx+1=a(x-x1)(x-x2),
令x=-1得:a(-1-x1)(-1-x2)=a-b+1,
即a(1+x1)(1+x2)=a-b+1,
∵-1<x1<x2<0,
∴1+x1>0,1+x2>0,
即(1+x1)(1+x2)>0,
∴a(1+x1)(1+x2)=a-b+1>0,
而a,b为正整数,则a(1+x1)(1+x2)=a-b+1≥1,
而x1x2= ,
,
∴a2(1+x1)(1+x2)x1x2=a-b+1≥1,
∴a2≥ ,
,
由于0<(1+x1)(-x1)=- +
+
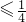 ,当
,当 时取最大值;
时取最大值;
同理0<(1+x2)(-x2)=- +
+ ,当x2=
,当x2= 时取最大值;
时取最大值;
而-1<x1<x2<0,
∴0<(1+x1)(1+x2)x1x2=(1+x1)(-x1)(1+x2)(-x2)< ,
,
从而a2≥ >16,
>16,
而a为正整数,所以a的最小值为5,
由于x1,x2为方程ax2+bx+1=0的两实根,则b2-4a>0,
∴b>2 >4,
>4,
∴正整数b的最小值为5,
当a=b=5时,ax2+bx+1=0的根为x= ,
,
∴x1= ,x2=
,x2= .
.
分析:先根据根与系数的关系得到x1+x2= ,x1x2=
,x1x2= ,再利用-1<x1<x2<0得到(1+x1)(1+x2)>0,进而得到(1+x1)(1+x2)=1+x1+x2+x1x2=1-
,再利用-1<x1<x2<0得到(1+x1)(1+x2)>0,进而得到(1+x1)(1+x2)=1+x1+x2+x1x2=1- =
= >0,可推出a、b的取值范围值,进而求出a、b的值.
>0,可推出a、b的取值范围值,进而求出a、b的值.
点评:此题考查了抛物线与x轴的交点坐标,根据函数特点及根与系数的关系得到关于a、b的不等式,再求出其具体值是解题的重要环节.
则b2-4a>0①
x1+x2=
 ,x1x2=
,x1x2= ②,
②,∵-1<x1<x2<0,
∴1+x1>0,1+x2>0,
即(1+x1)(1+x2)>0,
∴(1+x1)(1+x2)=1+x1+x2+x1x2=1-
 =
= >0,
>0,而a>0,
∴a-b+1>0,即:a>b+1,又a,b都是正整数,则a≥b③,
由①得,b>2
 ④,
④,由③、④得a>2
 ,即
,即 >2,
>2,∴a>4,因此正整数a的最小值为5.
由④得:b>2
 >4,
>4,∴正整数b的最小值为5,
当a=b=5时,ax2+bx+1=0的根为x=
 ,
,∴
 ,
,
解法2:依题意:y=ax2+bx+1=a(x-x1)(x-x2),
令x=-1得:a(-1-x1)(-1-x2)=a-b+1,
即a(1+x1)(1+x2)=a-b+1,
∵-1<x1<x2<0,
∴1+x1>0,1+x2>0,
即(1+x1)(1+x2)>0,
∴a(1+x1)(1+x2)=a-b+1>0,
而a,b为正整数,则a(1+x1)(1+x2)=a-b+1≥1,
而x1x2=
 ,
,∴a2(1+x1)(1+x2)x1x2=a-b+1≥1,
∴a2≥
 ,
,由于0<(1+x1)(-x1)=-
 +
+
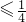 ,当
,当 时取最大值;
时取最大值;同理0<(1+x2)(-x2)=-
 +
+ ,当x2=
,当x2= 时取最大值;
时取最大值;而-1<x1<x2<0,
∴0<(1+x1)(1+x2)x1x2=(1+x1)(-x1)(1+x2)(-x2)<
 ,
,从而a2≥
 >16,
>16,而a为正整数,所以a的最小值为5,
由于x1,x2为方程ax2+bx+1=0的两实根,则b2-4a>0,
∴b>2
 >4,
>4,∴正整数b的最小值为5,
当a=b=5时,ax2+bx+1=0的根为x=
 ,
,∴x1=
 ,x2=
,x2= .
.分析:先根据根与系数的关系得到x1+x2=
 ,x1x2=
,x1x2= ,再利用-1<x1<x2<0得到(1+x1)(1+x2)>0,进而得到(1+x1)(1+x2)=1+x1+x2+x1x2=1-
,再利用-1<x1<x2<0得到(1+x1)(1+x2)>0,进而得到(1+x1)(1+x2)=1+x1+x2+x1x2=1- =
= >0,可推出a、b的取值范围值,进而求出a、b的值.
>0,可推出a、b的取值范围值,进而求出a、b的值.点评:此题考查了抛物线与x轴的交点坐标,根据函数特点及根与系数的关系得到关于a、b的不等式,再求出其具体值是解题的重要环节.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
设a,b都是正整数,且a-b、3b、a+b(a>2b)构成一直角三角形三边的长,则这个三角形的任一边的长不可能是( )
| A、12 | B、13 | C、14 | D、15 |
设x、y都是正整数,且满足y=
+
,则y的值不可能是( )
| x-16 |
| x+200 |
| A、18 | B、34 | C、54 | D、108 |