题目内容
18. 如图,在⊙O中,半径OA垂直于弦BC,垂足为D,OD=4,AD=1,求BC和AB的长.
如图,在⊙O中,半径OA垂直于弦BC,垂足为D,OD=4,AD=1,求BC和AB的长.
分析 连接OB,根据垂径定理得到BC=2BD,然后根据勾股定理即可得到结论.
解答  解:连接OB,
解:连接OB,
∵半径OA垂直于弦BC,
∴BC=2BD,
∵OD=4,AD=1,
∴OB=5,
∴BD=$\sqrt{B{O}^{2}-O{D}^{2}}$=3,
∴BC=6,AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{10}$.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
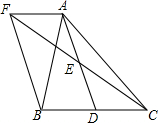 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. 某五金厂生产的螺母形状如图所示,
某五金厂生产的螺母形状如图所示,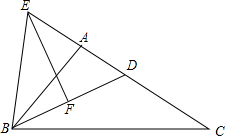 已知,在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于E,求证:∠EBA=∠C.
已知,在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于E,求证:∠EBA=∠C.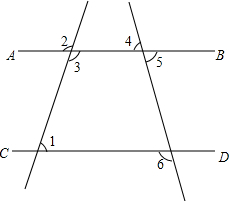 已知|3m-2n+60|与(7m-3n-60)2互为相反数,且m、n的值分别是图中∠1与∠2的度数,如果∠4=70°,试求∠6的度数.
已知|3m-2n+60|与(7m-3n-60)2互为相反数,且m、n的值分别是图中∠1与∠2的度数,如果∠4=70°,试求∠6的度数.