题目内容
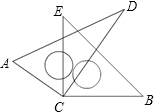
如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,
求证:∠CED+∠ACB=180°.请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G、D(已知)
∴∠FGB=∠CDB=90°( ),
∴GF∥CD ( ).
∵GF∥CD(已证)
∴∠2=∠BCD ( )
又∵∠1=∠2(已知),
∴∠1=∠BCD ( ),
∴ ,( )
∴∠CED+∠ACB=180° .


【考点】平行线的判定与性质.
【专题】推理填空题.
【分析】由FG⊥AB,CD⊥AB,得到∠FGB=∠CDB=90°,根据平行线的判定和性质得到∠2=∠BCD 由等量代换得到∠1=∠BCD,证出DE∥BC,从而证得结论.
【解答】证明:∵FG⊥AB,CD⊥AB,垂足分别为G、D(已知)
∴∠FGB=∠CDB=90°( 垂直的定义),
∴GF∥CD ( 同位角相等,两直线平行).
∵GF∥CD(已证)
∴∠2=∠BCD ( 两直线平行,同位角相等)
又∵∠1=∠2(已知),
∴∠1=∠BCD ( 等量代换),
∴DE∥BC,(内错角相等,两直线平行)
∴∠CED+∠ACB=180.(两直线平行,同旁内角互补)
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;DE∥BC;内错角相等,两直线平行;两直线平行,同旁内角互补.
【点评】本题考查了平行线的判定与性质,属于基础题,关键是正确利用平行线的性质与判定定理证明.

练习册系列答案
相关题目

 a2•(﹣6ab)的结果正确的是( )
a2•(﹣6ab)的结果正确的是( )