��Ŀ����
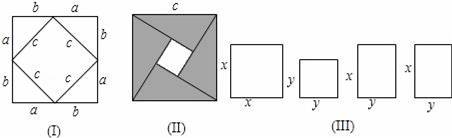
��������ͼ��I��ͼ�д������ε�����ɱ�ʾΪ��a+b��2��Ҳ�ɱ�ʾΪc2+4��
 ab������a+b��2=c2+4��
ab������a+b��2=c2+4��
 ab�ɴ��Ƶ���һ����Ҫ�Ľ���a2+b2=c2�������Ҫ�Ľ��۾��������ġ����ɶ����������ָ���ͼ�ο��Լ���ֱ�����ۻ���֤��ѧ���ɺ�ʽ�ķ�������ơ�����֤������
ab�ɴ��Ƶ���һ����Ҫ�Ľ���a2+b2=c2�������Ҫ�Ľ��۾��������ġ����ɶ����������ָ���ͼ�ο��Լ���ֱ�����ۻ���֤��ѧ���ɺ�ʽ�ķ�������ơ�����֤������
��1��������ͼ����2002��������ּҴ���꣩���������ʽ��֤���ɶ����������ĸ�ֱ�������εĽϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc����
��2�������ã����ṩ��ͼ�ν�����ϣ������ͼ�ε��������ʽ��֤����x+y��2=x2+2xy+y2
��3�������㹻��ı߳�Ϊx��С�����Σ��߳�Ϊy�Ĵ��������Լ���Ϊx��Ϊy�ij����Σ������Լ����ͼ�ε���ϣ������������ʽ��֤����x+y����x+2y��=x2+3xy+2y2��

�����㡿���ɶ�����֤��������ʽ�˶���ʽ����ȫƽ����ʽ�ļ��α�����
����������1��������Ӱ���ֵ����=�������ε������С�����ε����=4��ֱ�������ε����������֤����
��2������ƴ��һ���߳���x+y�������Σ����������߳��ֱ���x��y�������κ������������ֱ���x��y�ij�������ɣ�
��3������ƴ��һ���������ֱ���x+y��x+2y�ij����Σ����ɱ߳���x�������Σ��Լ��߳�Ϊy�������κͳ����ֱ���x��y�ľ��ν����ó��𰸣�
����𡿽⣺��1���������ε����Ϊ��c2���м�հײ������������Ϊ����b��a��2��
�ĸ���Ӱ����ֱ�������������Ϊ��4��
 ab��
ab��
��ͼ�ι�ϵ��֪�������������=�հ����������+��ֱ����������������У�
c2=��b��a��2+4��
 ab=b2��2ab+a2+2ab=a2+b2��
ab=b2��2ab+a2+2ab=a2+b2��
��2����ͼ1��ʾ���������α߳�Ϊ��x+y���������Ϊ����x+y��2��
�������Ҳ���������߳��ֱ�Ϊx��y��������Ϊx��Ϊy�ľ������֮�ͣ�
��x2+2xy+y2
��������x+y��2=x2+2xy+y2������
��3����ͼ2��ʾ������εij������ֱ�Ϊ��x+y������x+2y�����������Ϊ����x+y��•��x+2y����
��ͼ�ι�ϵ�Ͽɵô����Ϊһ���߳�Ϊx���������Լ�2���߳�Ϊy�������κ�����С���ι��ɵ���������ֿɱ�ʾΪ��
x2+3xy+2y2��
������x+y����x+2y��=x2+3xy+2y2��




��������������Ҫ�����˹��ɶ�����֤����ע����������ͨ����ͬ�ķ�������ͬһ��ͼ�ε������֤��һЩ��ʽ�ķ�����
��

 ʱ��c��ֵΪ__________��
ʱ��c��ֵΪ__________��

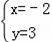
 ����k=��
����k=��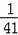
 C��
C��
 �Ĵ����ǣ�������
�Ĵ����ǣ������� �Ƕ��κ�������m=��������������
�Ƕ��κ�������m=��������������