��Ŀ����
 ��֪��ƽ��ֱ������ϵ����A��a��0����B��0��-b����C��b��0�����㣬��a��b��0��������y=��x-2����x-m��-��n-2����n-m���� ��m��nΪ��������m+2��2n��0����������A�͵�C������ΪP
��֪��ƽ��ֱ������ϵ����A��a��0����B��0��-b����C��b��0�����㣬��a��b��0��������y=��x-2����x-m��-��n-2����n-m���� ��m��nΪ��������m+2��2n��0����������A�͵�C������ΪP��1����m��n����ʲô��ϵʱ��S��AOB���
��3����ͼ������ACPΪֱ��������ʱ���ж����������Ƿ���ȷ����ֱ��������DEF���������㶼�������������ϣ���DF��x�ᣬ��ô��ACP���DEFб���ϵĸ���ȡ��������ȷ������֤��������ȷ��ٳ�������
��������1����������y=��x-2����x-m��-��n-2����n-m����������εã�y=��x-n����x+n-m-2��������m+2��2n��0�������߾�����A�͵�C��������a��b��ֵ���ɵ�S��AOB=
ab=
��m+2-n��n����ɵõ�m+2=2nʱ��S��AOB���
��2���ɵ���ACP��ֱ��������ʱ��AP��CP����|AC|����P�㵽x������2����������y=��x-n����x+n-m-2�����ɵö����Ȼ��x���·�����ɵ�[��m+2��-2n][��m+2��-��2n+2��]=0���ɵ�A��C������ͬһ�㣬���ɵ�m=2n������ԭ������õ�A��n+2��0������C��n��0������P��n+1��-1����Ȼ����������������DE��x�ᣬ��D��E���������Ϊy=b�����������������ֱ�Ϊ��D��n+1-
��b����E��n+1+
��b�������F����Ϊ��x0��y0�����������y0��ֵ�����F��б��DE�ľ���Ϊb-��b-1��=1������P��б��AC����һ��������֤��ԭ��������ȷ�ģ�
| 1 |
| 2 |
| 1 |
| 2 |
��2���ɵ���ACP��ֱ��������ʱ��AP��CP����|AC|����P�㵽x������2����������y=��x-n����x+n-m-2�����ɵö����Ȼ��x���·�����ɵ�[��m+2��-2n][��m+2��-��2n+2��]=0���ɵ�A��C������ͬһ�㣬���ɵ�m=2n������ԭ������õ�A��n+2��0������C��n��0������P��n+1��-1����Ȼ����������������DE��x�ᣬ��D��E���������Ϊy=b�����������������ֱ�Ϊ��D��n+1-
| b+1 |
| b+1 |
����⣺��1����y=��x-2����x-m��-��n-2����n-m��=��x-n����x+n-m-2����
�֡�m+2��2n����m+2-n��n��
��㣨m+2-n��0���ڵ㣨n��0���ұߣ�
�������߹�A���C�㣬
��a=m+2-n��b=n��
��S��AOB=
ab=
��m+2-n��n��
[
��m+2-n��+n]2=
��m+2��2��
���ҽ���m+2-n=nʱȡ��=������ʱm+2=2n��
��m+2=2nʱ��S��AOB���
��2��������ȷ��
���ɣ��ߵ���ACP��ֱ��������ʱ��AP��CP����|AC|����P�㵽x������2����
�֡�������y=��x-n����x+n-m-2��=[x-
��m+2��]2-
��m+2��2+n��m+2-n����
�ඥ���Ȼ��x���·���
���� 2[
��m+2��2-n��m+2-n��]=��m+2-n��-n��
����ã�[��m+2��-2n][��m+2��-��2n+2��]=0��
��ȻA��C������ͬһ�㣬
��m+2-n��n������m+2��-2n��0��
�ࣨm+2��-��2n+2��=0��
�ã�m=2n��
����ԭ������y=��x-n����x-n-2����
���A��n+2��0������C��n��0������P��n+1��-1����
�������������
��DE��x�ᣬ
���FΪRt��DEF��ֱ�ǣ�
��D��E���������Ϊy=b�����������������ֱ�Ϊ��D��n+1-
��b����E��n+1+
��b����
���F������x0��y0����
��DF��EF��
����
•
=-1��
����ã�x0-n-1��2+��y0-b��2=b+1��
�֣�x0��y0������y0=��x0-n����x0-n-2��=[��x0-n-1��+1][��x0-n-1��-1]=��x0-n-1��2-1��
������ʽ��ȥx0����ã�y02+��1-2b��y0+��b2-b��=0��
���y0=b��b-1����ȥy0=b����y0=b-1��
��F��б��DE�ľ���Ϊb-��b-1��=1������P��б��AC����һ����
�ۺ���������������ȷ�ģ�
�֡�m+2��2n����m+2-n��n��
��㣨m+2-n��0���ڵ㣨n��0���ұߣ�
�������߹�A���C�㣬
��a=m+2-n��b=n��
��S��AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
���ҽ���m+2-n=nʱȡ��=������ʱm+2=2n��
��m+2=2nʱ��S��AOB���
��2��������ȷ��
���ɣ��ߵ���ACP��ֱ��������ʱ��AP��CP����|AC|����P�㵽x������2����
�֡�������y=��x-n����x+n-m-2��=[x-
| 1 |
| 2 |
| 1 |
| 4 |
�ඥ���Ȼ��x���·���
���� 2[
| 1 |
| 4 |
����ã�[��m+2��-2n][��m+2��-��2n+2��]=0��
��ȻA��C������ͬһ�㣬
��m+2-n��n������m+2��-2n��0��
�ࣨm+2��-��2n+2��=0��
�ã�m=2n��
����ԭ������y=��x-n����x-n-2����
���A��n+2��0������C��n��0������P��n+1��-1����
�������������
��DE��x�ᣬ
���FΪRt��DEF��ֱ�ǣ�
��D��E���������Ϊy=b�����������������ֱ�Ϊ��D��n+1-
| b+1 |
| b+1 |
���F������x0��y0����
��DF��EF��
����
| y0-b | ||
x0-(n+1-
|
| y0-b | ||
x0-(n+1+
|
����ã�x0-n-1��2+��y0-b��2=b+1��
�֣�x0��y0������y0=��x0-n����x0-n-2��=[��x0-n-1��+1][��x0-n-1��-1]=��x0-n-1��2-1��
������ʽ��ȥx0����ã�y02+��1-2b��y0+��b2-b��=0��
���y0=b��b-1����ȥy0=b����y0=b-1��
��F��б��DE�ľ���Ϊb-��b-1��=1������P��б��AC����һ����
�ۺ���������������ȷ�ģ�
���������⿼���˴���ϵ��������κ����Ľ���ʽ���䷽����һԪ���η��̣�ֱ�������ε������Լ��㵽ֱ�ߵľ����֪ʶ�������ۺ��Ժ�ǿ���ѶȽϴ���Ĺؼ��Ƿ���˼�������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
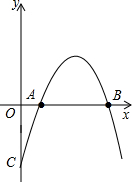 ���κ���y=ax2+bx+c��a��0����ͼ����A��B����y���ཻ�ڵ�C��
���κ���y=ax2+bx+c��a��0����ͼ����A��B����y���ཻ�ڵ�C�� ��2013•�㽭һģ����ͼ����֪��ƽ��ֱ������ϵ�У���A��4��0����B��-3��0������C��y���������ϣ���tan��CAO=1����Q���߶�AB�ϵĶ��㣬����Q��QE��AC��BC�ڵ�E��
��2013•�㽭һģ����ͼ����֪��ƽ��ֱ������ϵ�У���A��4��0����B��-3��0������C��y���������ϣ���tan��CAO=1����Q���߶�AB�ϵĶ��㣬����Q��QE��AC��BC�ڵ�E��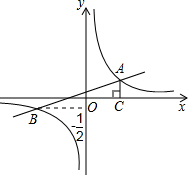 ��2012•������ģ�⣩��ͼ����֪��ƽ��ֱ������ϵxOy�У�һ�κ���y1=kx+b��k��0����ͼ���뷴��������y2=
��2012•������ģ�⣩��ͼ����֪��ƽ��ֱ������ϵxOy�У�һ�κ���y1=kx+b��k��0����ͼ���뷴��������y2=