题目内容
3.(1)先化简,再求值:x2+2x-3(x2-$\frac{2}{3}$x),其中x=-$\frac{1}{2}$.(2)计算:$\frac{1}{2}$xy-2(xy-$\frac{1}{3}$xy2)+($\frac{3}{2}$xy+$\frac{1}{3}$xy2),其中x、y满足|x-6|+(y+2)2=0.
分析 (1)原式去括号合并得到最简结果,把x的值代入计算即可求出值;
(2)原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:(1)原式=x2+2x-3x2+2x=-2x2+4x,
当x=-$\frac{1}{2}$时,原式=-$\frac{1}{2}$-2=-2$\frac{1}{2}$;
(2)原式=$\frac{1}{2}$xy-2xy+$\frac{2}{3}$xy2+$\frac{3}{2}$xy+$\frac{1}{3}$xy2=xy2,
由|x-6|+(y+2)2=0,得到x=6,y=-2,
则原式=24.
点评 此题考查了整式的加减-化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列各组图形中,成轴对称的两个图形是( )
| A. |  | B. |  | C. |  | D. |  |
8.国家提倡“低碳减排”,某公司计划在海边建风能发电站,电站年均发电量约为216000000度,将数据216000000用科学记数法表示为( )
| A. | 216×106 | B. | 21.6×107 | C. | 2.16×108 | D. | 2.16×109 |
 如图所示,抛物线y=ax2-x+c的图象经过A(-1,0)、B(0,-2)两点.
如图所示,抛物线y=ax2-x+c的图象经过A(-1,0)、B(0,-2)两点.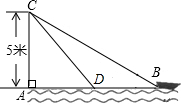 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)