题目内容
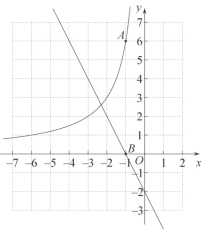
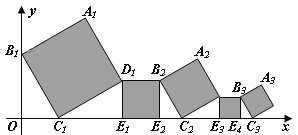
【题目】如图，在平面直角坐标系中放置5个正方形，点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3在x轴上．若正方形A1B1C1D1的边长为1，∠B1C1O﹦60，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
根据两直线平行，同位角相等可得∠B3C3O＝∠B2C2O＝∠B1C1O＝60°，然后解直角三角形求出OC1、C1E、E1E2、E2C2、C2E3、E3E4、E4C3，再求出B3C3，过点A3延长正方形的边交x轴于M，过点A3作A3N⊥x轴于N，先求出A3M，再解直角三角形求出A3N，得出点A3到x轴的距离．
解：如图，∵B1C1∥B2C2∥B3C3，
∴∠B3C3O＝∠B2C2O＝∠B1C1O＝60°，
∵正方形A1B1C1D1的边长为1，
∴OC1＝
，
C1E＝
，
E1E2＝，
E2C2＝
，
C2E3＝E2B2＝
，
E3E4＝，
E4C3＝
，
∴B3C3＝2E4C3＝2×
，
过点A3延长正方形的边交x轴于M，过点A3作A3N⊥x轴于N，
则A3M＝
，
A3N＝A3Msin60°＝
，
∴点A3到x轴的距离是：
，
故选：D．
练习册系列答案
相关题目
