题目内容
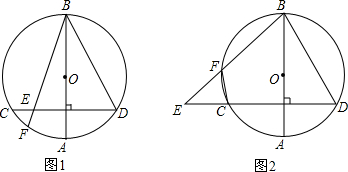
16.如图1,⊙O中,直径AB垂直于CD,E为线段CD上一点,BE交⊙O于F.(1)求证:∠BFC+∠ABD=90°;
(2)如图2,若点E在DC的延长线上,其他条件不变,试探究:∠BFC与∠ABD之间的数量关系.
分析 (1)先利用垂直的定义得到∠D+∠ABD=90°,再根据圆周角定理得∠D=∠BFC,所以∠BFC+∠ABD=90°;
(2)先利用圆内接四边形的性质得∠BFC+∠D=180°,加上∠D+∠ABD=90°,然后把两等式相减即可得到∠BFC-∠ABD=90°.
解答 (1)证明:∵AB⊥CD,
∴∠D+∠ABD=90°,
而∠D=∠BFC,
∴∠BFC+∠ABD=90°;
(2)解:∵∠BFC+∠D=180°,
而∠D+∠ABD=90°,
∴∠BFC-∠ABD=90°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
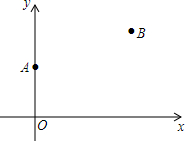 在一条公路的同侧有两个村庄A,B,若在公路上建一个加油站P,使得加油站到两个村庄的距离之和最小,即PA+PB最小.设公路为x轴,A点的坐标为(0,3),B点的坐标为(6,5).
在一条公路的同侧有两个村庄A,B,若在公路上建一个加油站P,使得加油站到两个村庄的距离之和最小,即PA+PB最小.设公路为x轴,A点的坐标为(0,3),B点的坐标为(6,5).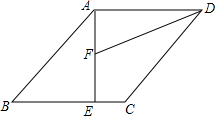 如图,已知平行四边形ABCD,AE⊥AD,AE=AD,DF平分∠ADC交AE于F,且AF=EF.若BE=3,求CE=1.
如图,已知平行四边形ABCD,AE⊥AD,AE=AD,DF平分∠ADC交AE于F,且AF=EF.若BE=3,求CE=1.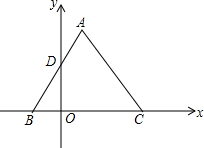 如图是边长为4的等边△ABC,如果以BC所在直线为x轴,y轴经过AB的中点D点,请你求出点A、B、C的坐标.
如图是边长为4的等边△ABC,如果以BC所在直线为x轴,y轴经过AB的中点D点,请你求出点A、B、C的坐标.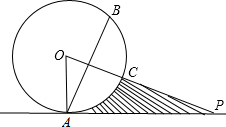 如图,点P在圆O外,PA与圆O相切于C点,点B与点A关于直线PO对称,已知OA=4,∠P=30°,求:
如图,点P在圆O外,PA与圆O相切于C点,点B与点A关于直线PO对称,已知OA=4,∠P=30°,求: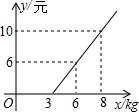 汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示.
汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示.