Question

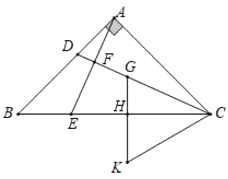
【题目】如图，已知是线段上的两点，，，．以为圆心以为半径作圆弧，以为圆心以为半径作圆弧，两圆弧相交于点构成，设．

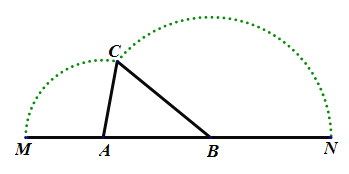
（1）求的取值范围；

（2）若为直角三角形，求的值；

（3）当是锐角时，求的最大面积？

Answer 1

【答案】（1）；（2）当或时，△ABC是直角三角形；（3）△ABC的最大面积为

【解析】

（1）根据三角形的三边关系，列出关于x的不等式组，可以求得x的取值范围；

（2）分类讨论直角三角形ABC，根据勾股定理列方程，根据根的情况确定直角三角形的存在性；

（3）把△ABC的面积S的问题，转化为S2的问题．然后利用勾股定理求出S2与x的函数关系式，再利用二次函数求最值即可．

解：（1）在△ABC中，，，，

∴

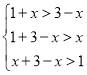
解得．

（2）①若AC为斜边，则，

即，

此方程无实根；

②若AB为斜边，则，

解得，满足．

③若BC为斜边，则，

解得，满足．

因此当或时，△ABC是直角三角形．

（3）在△ABC中，作于D，

设CD=h，△ABC的面积为S，则S=．

∵AD＋BD=AB

∴．

移项，得．

两边平方，得．

整理，得．

两边平方，得．

整理，得

所以．

∵是锐角

∴

当时（满足），取最大值，从而S取最大值．

即△ABC的最大面积为．