题目内容
已知:关于x的方程x2-2(m+1)x+m2=0
(1)当m取何值时,方程有两个实数根?
(2)当m=1时,解此方程.
(1)当m取何值时,方程有两个实数根?
(2)当m=1时,解此方程.
考点:根的判别式
专题:
分析:(1)求出b2-4ac的值,即可得出不等式,求出即可;
(2)代入后解一元二次方程,即可得出答案.
(2)代入后解一元二次方程,即可得出答案.
解答:解:(1)△=[-2(m+1)]2-4×1×m2=8m+4
∵方程有两个实数根
∴△≥0
即8m+4≥0
∴m≥-
;
(2)当x=1时,方程为x2-4x+1=0
移项,得:x2-4x=-1,
配方得:x2-4x+22=-1+22,
(x-2)2=3,
∴x1=2+
,x2=2-
.
∵方程有两个实数根
∴△≥0
即8m+4≥0
∴m≥-
| 1 |
| 2 |
(2)当x=1时,方程为x2-4x+1=0
移项,得:x2-4x=-1,
配方得:x2-4x+22=-1+22,
(x-2)2=3,
∴x1=2+
| 3 |
| 3 |
点评:本题考查了解一元二次方程,一元二次方程的根的判别式的应用,注意:当b2-4ac≥0时,一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0)有两个实数根,当b2-4ac<0时,一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0)无实数根.

练习册系列答案
相关题目
已知(a3b-4)2÷(-ab-3)3=3,则a9b3的值是( )
| A、-9 | B、9 | C、27 | D、-27 |
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?若设每轮传染中平均一个人传染了x个人,那么x满足的方程是( )
| A、x(1+x)=121 |
| B、1+x(1+x)=121 |
| C、x+x(1+x)=121 |
| D、1+x+x(1+x)=121 |
下列运算中,正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知D是△ABC内一点,且BD=CD,下列说法正确的是( )
| A、点D是三角形三边垂直平分线的交点 |
| B、点D是三角形三条角平分线的交点 |
| C、点D在BC的垂直平分线上 |
| D、点D在∠A的平分线上 |
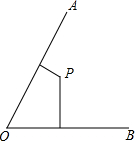 已知∠AOB=60°,P为角内部一点,P到OA、OB的距离分别为1和5,在射线OA上找一点M,在射线OB上找一点N,使PM+PN最小,则最小值为
已知∠AOB=60°,P为角内部一点,P到OA、OB的距离分别为1和5,在射线OA上找一点M,在射线OB上找一点N,使PM+PN最小,则最小值为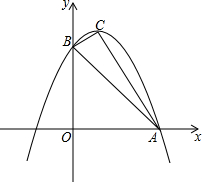 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.