题目内容
7．
如图，已知⊙O的半径为5，弦AB=8，则圆心O到AB的距离是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 如图，作OE⊥AB于E．根据垂径定理可得AE=4，利用勾股定理可以求出OE．
解答 解：如图，作OE⊥AB于E．
∵OE⊥AB，AB=8
∴AE=EB=$\frac{1}{2}$AB=4，
在Rt△AOC中，∵∠AEO=90°，OA=5．AE=4，
∴OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3．
故选C．
点评 本题考查垂径定理、勾股定理等知识，解题的关键是学会添加辅助线，构造直角三角形解决问题，属于中考常考题型．
练习册系列答案
灵星计算小达人系列答案
相关题目
17．
如图，在△ABC和△DEF中，给出以下六个条件中，以其中三个作为已知条件，不能判断△ABC和△DEF全等的是（ ）
①AB=DE；②BC=EF；③AC=DF；④∠A=∠D；⑤∠B=∠E；⑥∠C=∠F．
如图，在△ABC和△DEF中，给出以下六个条件中，以其中三个作为已知条件，不能判断△ABC和△DEF全等的是（ ）①AB=DE；②BC=EF；③AC=DF；④∠A=∠D；⑤∠B=∠E；⑥∠C=∠F．
| A． | ①⑤② | B． | ①②③ | C． | ④⑥① | D． | ②③④ |
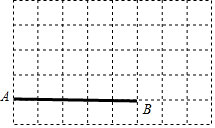如图，在8×5的正方形网格中（小正方形的边长均为1）有线段AB，其端点均在小正方形的顶点上，请按要求在方格纸中画出图形：
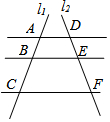如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F．若AB=1，BC=2，DE=1.5，则EF的长为（ ）
17．在△ABC中，∠A=30°，∠B=75°，则△ABC是（ ）
| A． | 直角三角形 | B． | 钝角三角形 | C． | 等边三角形 | D． | 等腰三角形 |