题目内容
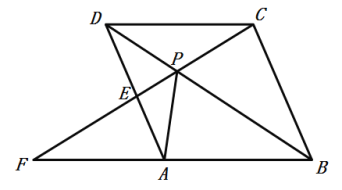
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径在矩形
为直径在矩形![]() 内作半圆
内作半圆![]() .
.
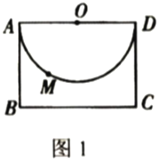
(1)若点![]() 是半圆
是半圆![]() 上一点,则点
上一点,则点![]() 到
到![]() 的最小距离为________;
的最小距离为________;
(2)如图2,保持矩形![]() 固定不动,将半圆
固定不动,将半圆![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]()
![]() 度,得到半圆
度,得到半圆![]() ,则当半圆
,则当半圆![]() 与
与![]() 相切时,求旋转角
相切时,求旋转角![]() 的度数;
的度数;

(3)在旋转过程中,当![]() 与边
与边![]() 有交点时,求
有交点时,求![]() 的取值范围.
的取值范围.
【答案】(1)1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,时
,时![]() 即为点
即为点![]() 到
到![]() 的最小距离.推出四边形
的最小距离.推出四边形![]() 是矩形,即可求出点
是矩形,即可求出点![]() 到
到![]() 的最小距离;
的最小距离;
(2)设半圆![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,延长
,延长![]() 、
、![]() 交于点
交于点![]() ,证明
,证明![]() ,解得
,解得![]() ,根据
,根据![]() 中,
中,![]() ,
,![]() ,即可求出旋转角
,即可求出旋转角![]() 的度数;
的度数;
(3)分别求出当点![]() 在
在![]() 上时和当
上时和当![]() 与边
与边![]() 相切时的
相切时的![]() 的值,即可求出
的值,即可求出![]() 的取值范围.
的取值范围.
(1)如图1,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
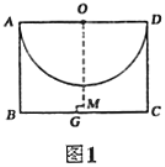
此时![]() 即为点
即为点![]() 到
到![]() 的最小距离.
的最小距离.
∵四边形![]() 是矩形,点
是矩形,点![]() 在
在![]() 上,且
上,且![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
故答案为:1.
(2)如图2,设半圆![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,延长
,延长![]() 、
、![]() 交于点
交于点![]() ,
,
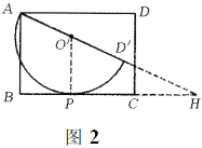
∴![]() 于点
于点![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ;
;
(3)当点![]() 在
在![]() 上时,如图3,
上时,如图3,
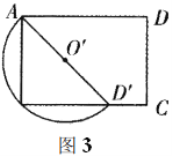
∵![]() ,
,![]() 是半圆
是半圆![]() 的直径,
的直径,
∴点![]() 在
在![]() 上,
上,
∵在![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,
∴由勾股定理得![]() ,
,
∴![]() ,
,
又∵当![]() 与边
与边![]() 相切时,
相切时,![]() ,
,
∴此时![]() ,
,
∴当![]() 与边
与边![]() 有交点时,
有交点时,![]() .
.

【题目】在建设港珠澳大桥期间,大桥的规划选线须经过中华白海豚国家级白然保护区—区域![]() 或区域
或区域![]() .为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海
.为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海![]() 天,在区域
天,在区域![]() 、
、![]() 两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
(收集数据)
连续![]() 天观察中华白海豚每天在区域
天观察中华白海豚每天在区域![]() 、区域
、区域![]() 出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(整理、描述数据)
(1)按如下数段整理、描述这两组数据,请补充完整:
海豚数 |
|
|
|
|
|
区域 |
|
|
| _________ | _________ |
区域 |
|
|
|
|
|
(2)两组数据的平均数、中位数,众数如下所示:
观测点 | 平均数 | 中位数 | 众数 |
区域 |
|
|
|
区域 |
|
|
|
请填空:上表中中位数![]() _______,,众数
_______,,众数![]() ______;
______;
(3)规划者们选择了区域![]() 为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的
为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的![]() 天施工期内,区域
天施工期内,区域![]() 大约有多少天中华白海豚出现的数目在
大约有多少天中华白海豚出现的数目在![]() 的范围内?
的范围内?