题目内容
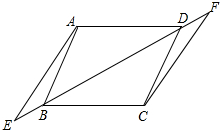 如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.
如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.考点:全等三角形的判定与性质,平行四边形的性质
专题:证明题
分析:根据平行四边形的对边相等可得AB=CD,AB∥CD,再根据两直线平行,内错角相等可得∠ABD=∠CDB,然后求出∠ABE=∠CDF,再利用“边角边”证明△ABE和△CDF全等,根据全等三角形对应边相等证明即可.
解答:证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴180°-∠ABD=180°-∠CDB,
即∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF.
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴180°-∠ABD=180°-∠CDB,
即∠ABE=∠CDF,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(SAS),
∴AE=CF.
点评:本题考查了全等三角形的判定与性质,平行四边形的性质,熟记性质与三角形全等的判定方法求出全等的条件是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
下列函数中,自变量x的取值范围是x>1且x≠3的是( )
A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
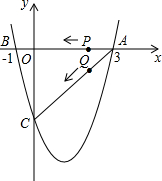 如图,二次函数y=
如图,二次函数y=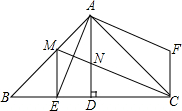 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
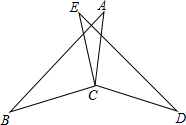 如图,已知:EC=AC,∠BCE=∠DCA,BC=DC;求证:AB=DE.
如图,已知:EC=AC,∠BCE=∠DCA,BC=DC;求证:AB=DE.