题目内容
15.如图1,我们在2016年1月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”).该十字星的十字差为12×14-6×20=48,再选择其它位置的十字星,可以发现“十字差”仍为48.(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为24.
(2)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.
(3)如图3,将正整数依次填入三角形的数表中,探究不同十字星的“十字差”,若某个十字星中心的数在第32行,且其相应的“十字差”为2015,则这个十字星中心的数为976(直接写出结果).

分析 (1)根据题意求出相应的“十字差”,即可确定出所求定值;
(2)定值为k2-1=(k+1)(k-1),理由为:设十字星中心的数为x,表示出十字星左右两数,上下两数,进而表示出十字差,化简即可得证;
(3)设正中间的数为a,则上下两个数为a-62,a+64,左右两个数为a-1,a+1,根据相应的“十字差”为2015求出a的值即可.
解答 解:(1)根据题意得:6×8-2×12=48-24=24;
故答案为:24;
(2)定值为k2-1=(k+1)(k-1);
证明:设十字星中心的数为x,则十字星左右两数分别为x-1,x+1,上下两数分别为x-k,x+k(k≥3),
十字差为(x-1)(x+1)-(x-k)(x+k)=x2-1-x2+k2=k2-1,
故这个定值为k2-1=(k+1)(k-1);
(3)设正中间的数为a,则上下两个数为a-62,a+64,左右两个数为a-1,a+1,
根据题意得:(a-1)(a+1)-(a-62)(a+64)=2015,
解得:a=976.
故答案为:976.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
6. 如图,点A,B,C是⊙O上的三点,已知∠AOB=110°,那么∠ACB的度数是( )
如图,点A,B,C是⊙O上的三点,已知∠AOB=110°,那么∠ACB的度数是( )
 如图,点A,B,C是⊙O上的三点,已知∠AOB=110°,那么∠ACB的度数是( )
如图,点A,B,C是⊙O上的三点,已知∠AOB=110°,那么∠ACB的度数是( )| A. | 50° | B. | 55° | C. | 70° | D. | 110° |
3.蔬菜种植户经过调查发现:若一种蔬菜加工后出售,单价可提高20%,但质量只有加工前的九折.现有未加工的这种蔬菜30千克,加工后可以比不加工多卖12元,这种蔬菜加工前每千克卖多少元?分析:请先填写下表,然后完成求解:
| 单价(元/千克) | 质量(千克) | 销售额(元) | |
| 加工前 | x | 30 | 30x |
| 加工后 | (1+20%)x | 30×90% | (1+20%)x×(30×90%) |
10. 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )
 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
20.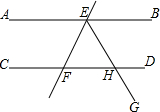 如图,直线AB∥CD,直线EF分别交直线AB、CD于E、F,∠BEF的平分线EG交CD于H.若∠EFH=50°,则∠BEH的度数为( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于E、F,∠BEF的平分线EG交CD于H.若∠EFH=50°,则∠BEH的度数为( )
 如图,直线AB∥CD,直线EF分别交直线AB、CD于E、F,∠BEF的平分线EG交CD于H.若∠EFH=50°,则∠BEH的度数为( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于E、F,∠BEF的平分线EG交CD于H.若∠EFH=50°,则∠BEH的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
4.下面是某同学在一次课堂测验中利用等式的性质解方程的过程,其中正确的是( )
| A. | x+5=26,得x=21 | B. | -5x=15,得x=-$\frac{1}{3}$ | ||
| C. | -$\frac{1}{3}$x-5=4,得$\frac{1}{3}$x=4+5 | D. | 5y-3y+y=9,得(5-3)y=9 |
 过直线l外一点P用直尺和圆规作直线l的垂线的方法是:以点P为圆心,大于点P到直线l的距离长为半径画弧,交直线l于点A、B;分别以A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点C.连结PC,则PC⊥AB.
过直线l外一点P用直尺和圆规作直线l的垂线的方法是:以点P为圆心,大于点P到直线l的距离长为半径画弧,交直线l于点A、B;分别以A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点C.连结PC,则PC⊥AB. 如图,直线l1的函数表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
如图,直线l1的函数表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C. 作图题
作图题