题目内容
8.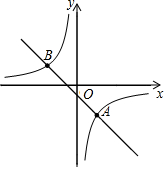 如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)交于点A(2,-3)和点B(n,2).
如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)交于点A(2,-3)和点B(n,2).(1)求直线与双曲线的表达式;
(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y=$\frac{m}{x}$(m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
分析 (1)把A的坐标代入可求出m,即可求出反比例函数解析式,把B点的坐标代入反比例函数解析式,即可求出n,把A,B的坐标代入一次函数解析式即可求出一次函数解析式;
(2)根据图象和函数解析式得出即可.
解答 解:(1)∵双曲线y=$\frac{m}{x}$(m≠0)经过点A(2,-3),
∴m=-6.
∴双曲线的表达式为y=-$\frac{6}{x}$.
∵点B(n,2)在双曲线y=-$\frac{6}{x}$上,
∴点B的坐标为(-3,2).
∵直线y=kx+b经过点A(2,-3)和点B(-3,2),
∴$\left\{\begin{array}{l}{2k+b=-3}\\{\;}\\{-3k+b=2}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-1}\\{\;}\\{b=-1}\end{array}\right.$,
∴直线的表达式为y=-x-1;
(2)符合条件的点P的坐标是(1,-6)或(6,-1).
点评 本题考查了一次函数和反比例函数的交点问题,关键是用待定系数法求一次函数的解析式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
19.在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.我市区机抽取了部分家庭,调查每月用于信息消费的金额,数据整理成如图所示的不完整统计图.已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题:
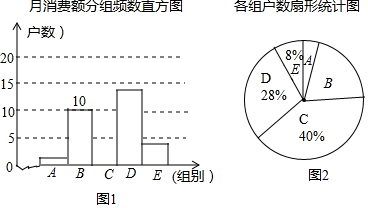
月消费额分组统计表
(1)A组的频数是2,本次调查样本的容量是50;
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额少于300元的户数是多少?

月消费额分组统计表
| 组别 | 消费额(x)元 |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额少于300元的户数是多少?
16. 实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
 实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )| A. | a | B. | b | C. | -b | D. | c |
3.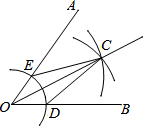 用尺规作图法作已知角∠AOB的平分线的步骤如下:
用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
 用尺规作图法作已知角∠AOB的平分线的步骤如下:
用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
13.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B.
如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B. 如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面2.4m,桌面距离地面0.8m(桌面厚度不计算),若桌面的面积是1.2m2,则地面上的阴影面积是2.7m2.
如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面2.4m,桌面距离地面0.8m(桌面厚度不计算),若桌面的面积是1.2m2,则地面上的阴影面积是2.7m2.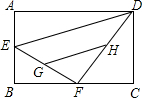 如图,在矩形ABCD中,AB=4,AD=6,点E是AB的中点,点F是BC边上的动点,连接EF,DF,G,H分别是EF和DF的中点,则GH的长为$\sqrt{10}$.
如图,在矩形ABCD中,AB=4,AD=6,点E是AB的中点,点F是BC边上的动点,连接EF,DF,G,H分别是EF和DF的中点,则GH的长为$\sqrt{10}$.