Question

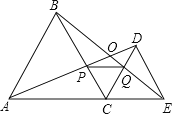
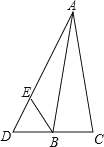
【题目】如图所示，已知△ABC 中，AB=AC，D 是 CB 延长线上一点，∠ADB=60°，E 是 AD上一点，E 是 AD的一点，且 DE=DB.求证：AE=BE+BC.

Answer 1

【答案】见解析

【解析】

首先延长DC到F，使CF=BD，连接AF，易得△ABD≌△ACF，继而可得△ADF是等边三角形，△DEB是等边三角形．则可证得结论．

证明：延长DC到F，使CF=BD，连接AF，

∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABD=∠ACF，
在△ABD和△ACF中，

∴△ABD≌△ACF（SAS），
∴AD=AF，
又∵∠ADB=60°，
∴△ADF是等边三角形，
∴AD=DF，
∵AD=AE+DE，DF=DB+BC+CF，
又∵DE=DB，且∠ADB=60°
∴△DEB是等边三角形．
∴DE=BE=DB=CF，
∴AE+DE=BE+BC+DE，
∴AE=BE+BC．