题目内容
【题目】已知
，点
为平面内一点，
于．
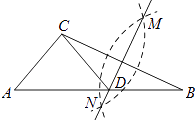
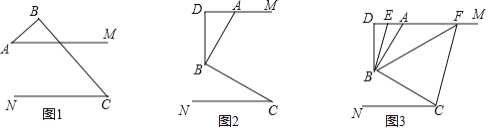
（1）如图1，直接写出
和
之间的数量关系 ；
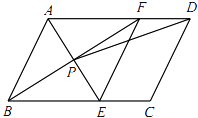
（2）如图2，过点作
于点
，求证：
；
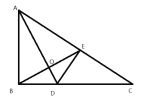
（3）如图3，在（2）问的条件下，点
、
在
上，连接
、
、
，平分
，平分
，若
，
，求
的度数．
【答案】（1）
；（2）见解析；（3）105°
【解析】
（1）根据平行线的性质以及直角三角形的性质进行证明即可；
（2）先过点
作
，根据同角的余角相等，得出
，再根据平行线的性质，得出
，即可得到
；
（3）先过点作，根据角平分线的定义，得出
，再设
，
，根据
，可得
，根据
，可得
，最后解方程组即可得到
，进而得出
．
解：（1）如图1，
，
，
，
，
，
故答案为：；
（2）如图2，过点作，
，
，即
，
又，
，
，
，
，
，
，
；
（3）如图3，过点作，
平分
，
平分
，
，
，
由（2）可得，
，
设，，则
，
，
，
，
，
，
，
，
中，由，可得
，①
由，可得
，②
由①②联立方程组，解得
，
，
．
练习册系列答案
相关题目
