题目内容
某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费10元时,床位可全部租出.若每张床位每天收费提高2元,则相应的减少了10张床位租出.如果每张床位每天以2元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
| A、14元 | B、15元 |
| C、16元 | D、18元 |
考点:二次函数的应用
专题:
分析:设每张床位提高x个单位,每天收入为y元,根据等量关系“每天收入=每张床的费用×每天出租的床位”可求出y与x之间的函数关系式,运用公式求最值即可.
解答:解:设每张床位提高x个2元,每天收入为y元.
则有y=(10+2x)(100-10x)
=-20x2+100x+1000.
当x=-
=2.5时,可使y有最大值.
又x为整数,则x=2时,y=1120;
x=3时,y=1120;
则为使租出的床位少且租金高,每张床收费=10+3×2=16(元).
故选C.
则有y=(10+2x)(100-10x)
=-20x2+100x+1000.
当x=-
| b |
| 2a |
又x为整数,则x=2时,y=1120;
x=3时,y=1120;
则为使租出的床位少且租金高,每张床收费=10+3×2=16(元).
故选C.
点评:本题考查了二次函数的实际应用,借助二次函数解决实际问题,利用二次函数对称性得出是解题关键.

练习册系列答案
相关题目
方程3x+2y=1和2x=y+3的公共解是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
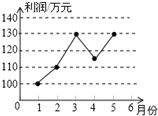 某企业1~5月份利润的变化情况图,以下说法中与图中反映的信息相符的是( )
某企业1~5月份利润的变化情况图,以下说法中与图中反映的信息相符的是( )| A、1~2月份利润的增长快于2~3月份利润的增长 |
| B、1~5月份利润的众数是130万元 |
| C、1~4月份利润的极差与1~5月份利润的极差不同 |
| D、1~5月份利润的中位数为120万元 |
已知,菱形的一条对角线与一条边的和是22,和这条边的差是2,若两对角线的长都是整数,则菱形的面积为( )
| A、96 | B、64 | C、60 | D、48 |
 如图,⊙O的直径CD与弦AB交于点M,CD⊥AB,AB=6,CD=10,OM=
如图,⊙O的直径CD与弦AB交于点M,CD⊥AB,AB=6,CD=10,OM=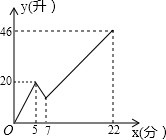 有一个附有进出水管的容器,每单位时间进、出的水量都是一定的.设从某一时刻开始5分钟内只进水不出水,在接着的2分钟内只出水不进水,又在随后的15分钟内既进水又出水,刚好将该容器注满.已知容器中的水量y升与时间x分之间的函数关系如图,则在第7分钟时容器内的水量为
有一个附有进出水管的容器,每单位时间进、出的水量都是一定的.设从某一时刻开始5分钟内只进水不出水,在接着的2分钟内只出水不进水,又在随后的15分钟内既进水又出水,刚好将该容器注满.已知容器中的水量y升与时间x分之间的函数关系如图,则在第7分钟时容器内的水量为


