题目内容
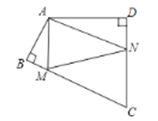
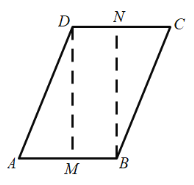
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
(1)当![]() 时,
时,![]() =_______度;
=_______度;
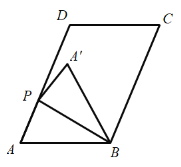
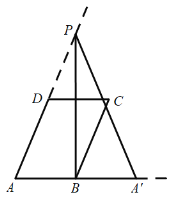
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
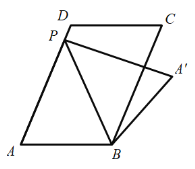
(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
【答案】(1)85或95或5;(2)![]() ;(3)
;(3)![]() 或9
或9
【解析】
(1)根据点P在线段AD上或AD的延长线上和点![]() 与AD的位置关系分类讨论,分别画出图形,根据折叠的性质即可求出结论;
与AD的位置关系分类讨论,分别画出图形,根据折叠的性质即可求出结论;
(2)根据平行四边形的性质可推出![]() ,从而得出
,从而得出![]() ,作
,作![]() 于
于![]() ,根据锐角三角函数和勾股定理求出AH和BH,利用锐角三角函数求出PH,即可求出结论;
,根据锐角三角函数和勾股定理求出AH和BH,利用锐角三角函数求出PH,即可求出结论;
(3)分点![]() 落在AD、BC、CD和AB上讨论,分别画出对应的图形,根据折叠的性质、锐角三角函数和勾股定理即可分别求出结论.
落在AD、BC、CD和AB上讨论,分别画出对应的图形,根据折叠的性质、锐角三角函数和勾股定理即可分别求出结论.
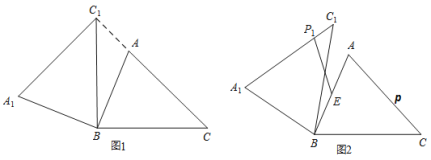
解:(1)①当点P在线段AD上,且点![]() 在直线AD右侧时,如下图所示
在直线AD右侧时,如下图所示

由折叠的性质可得![]() ;
;
②当点P在线段AD上,且点![]() 在直线AD左侧时,如下图所示
在直线AD左侧时,如下图所示
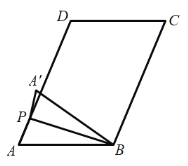
由折叠的性质可得![]() ;
;
③当点P在线段AD的延长线上时,如下图所示
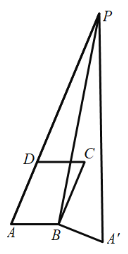
由折叠的性质可得![]()
综上:![]() =85°或95°或5°
=85°或95°或5°
故答案为:85或95或5;
(2)在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
作![]() 于
于![]() ,如下图,
,如下图,

∴![]() ,
,
∴设![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)①当点![]() 在
在![]() 上时,如下图,
上时,如下图,
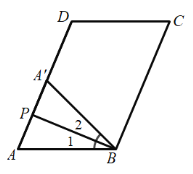
∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
设![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②当![]() 在
在![]() 上时,如下图
上时,如下图

由折叠可知,![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴四边形![]() 为菱形,
为菱形,
∴![]() ;
;
③当![]() 在CD上时,如下图,过点D作DM⊥AB于M,过点B作BN⊥CD于N
在CD上时,如下图,过点D作DM⊥AB于M,过点B作BN⊥CD于N
∴DM=BN,
∵![]()
设![]() ,
,![]() ,
,
∴![]() ,
,
解得:x=1
∴BN=DM=12
∵![]() 在CD上
在CD上
∴![]() ≥BN=12>BA
≥BN=12>BA
∴此种情况不存在;
④当![]() 在AB上时,如下图,根据折叠的性质可得点
在AB上时,如下图,根据折叠的性质可得点![]() 与点A关于PB对称,即点
与点A关于PB对称,即点![]() 在AB的延长线上,不符合题意.
在AB的延长线上,不符合题意.
综上:当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,
的边上时,![]() 或9;
或9;

【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.