题目内容
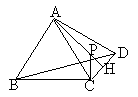
如图,AB=BC=CA=AD=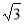 , AH⊥CD于H,CP⊥BC交AH于点P,AP=
, AH⊥CD于H,CP⊥BC交AH于点P,AP=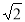 ,则BD=______.
,则BD=______.

【解析】
试题分析:设BD与AH交于点Q,则由AC=AD,AH⊥CD得∠ACQ=∠ADQ.又AB=AD,故∠ADQ=∠ABQ.从而∠ABQ=∠ACQ.可知A、B、C、P四点共圆.因为∠APC=90°+∠PCH=∠BCD,∠CBP=∠CAP,所以△APC∽△BCD,所以AC•BC=AP•BD,所以BD=AC•  ,所以BD=
,所以BD=  .故答案为:
.故答案为:  .
.

考点:1.相似三角形的判定与性质;2.确定圆的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.
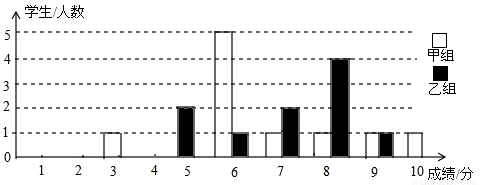
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组同学观点的理由.
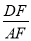 的值为( )
的值为( )
 的坡角由
的坡角由 减至
减至 .已知原坡面的长AB为6m(BC所在地面为水平面)
.已知原坡面的长AB为6m(BC所在地面为水平面)

 )
)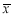 与方差s2如表所示,你认为表现最好的是( ).
与方差s2如表所示,你认为表现最好的是( ).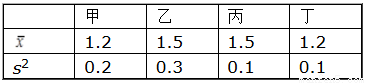
 的图像与x轴交于A、B,顶点为M,则S△ABM=_________.
的图像与x轴交于A、B,顶点为M,则S△ABM=_________. ,
, ,
,
 满足
满足 时,请你求出(1)中的代数式的值。
时,请你求出(1)中的代数式的值。