题目内容
化简与计算:
(1)
(2)
(3) +
+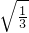 -2
-2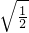
(4) -(π-2)0-|1-
-(π-2)0-|1- |
|
解:(1) ×
×
= =
=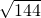 =12;
=12;
(2)( -
-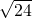 )÷
)÷ +(1-
+(1- )2
)2
= ÷
÷ -
-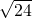 ÷
÷ +1-2
+1-2 +(
+( )2
)2
= -2+1-2
-2+1-2 +3
+3
=2- ;
;
(3) +
+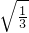 -2
-2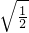
=2 +
+ -2×
-2×
=2 +
+ -
-
=3 +
+ ;
;
(4) -(π-2)0-|1-
-(π-2)0-|1- |
|
=3 -1-(
-1-( -1)
-1)
=3 -1-
-1- +1
+1
=2 .
.
分析:(1)利用二次根式的乘法法则 ×
× =
= (a≥0,b≥0)进行化简,把结果化为最简二次根式即可;
(a≥0,b≥0)进行化简,把结果化为最简二次根式即可;
(2)利用多项式除以单项式的方法把原式第一项变形,第二项利用完全平方公式展开,再利用二次根式的除法法则计算后,化为最简二次根式,合并同类二次根式即可得到结果;
(3)把原式的各项化为最简二次根式,合并同类二次根式后即可得到结果;
(4)原式第一项化为最简二次根式,第二项根据a0=1(a≠1)进行化简,第三项根据绝对值的代数意义,判断得到1- 小于0,得到绝对值等于它的相反数进行化简,去括号合并同类二次根式即可得到结果.
小于0,得到绝对值等于它的相反数进行化简,去括号合并同类二次根式即可得到结果.
点评:此题考查了二次根式的混合运算,零指数公式,以及绝对值的代数意义,二次根式的加减运算关键是合并同类二次根式,合并同类二次根式的化简是将二次根式化为最简二次根式,找出被开方数相同的二次根式,即同类二次根式;二次根式的乘除运算关键是运用二次根式的乘除运算法则.
 ×
×
=
 =
=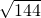 =12;
=12;(2)(
 -
-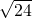 )÷
)÷ +(1-
+(1- )2
)2=
 ÷
÷ -
-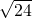 ÷
÷ +1-2
+1-2 +(
+( )2
)2=
 -2+1-2
-2+1-2 +3
+3=2-
 ;
;(3)
 +
+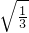 -2
-2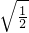
=2
 +
+ -2×
-2×
=2
 +
+ -
-
=3
 +
+ ;
;(4)
 -(π-2)0-|1-
-(π-2)0-|1- |
|=3
 -1-(
-1-( -1)
-1)=3
 -1-
-1- +1
+1=2
 .
.分析:(1)利用二次根式的乘法法则
 ×
× =
= (a≥0,b≥0)进行化简,把结果化为最简二次根式即可;
(a≥0,b≥0)进行化简,把结果化为最简二次根式即可;(2)利用多项式除以单项式的方法把原式第一项变形,第二项利用完全平方公式展开,再利用二次根式的除法法则计算后,化为最简二次根式,合并同类二次根式即可得到结果;
(3)把原式的各项化为最简二次根式,合并同类二次根式后即可得到结果;
(4)原式第一项化为最简二次根式,第二项根据a0=1(a≠1)进行化简,第三项根据绝对值的代数意义,判断得到1-
 小于0,得到绝对值等于它的相反数进行化简,去括号合并同类二次根式即可得到结果.
小于0,得到绝对值等于它的相反数进行化简,去括号合并同类二次根式即可得到结果.点评:此题考查了二次根式的混合运算,零指数公式,以及绝对值的代数意义,二次根式的加减运算关键是合并同类二次根式,合并同类二次根式的化简是将二次根式化为最简二次根式,找出被开方数相同的二次根式,即同类二次根式;二次根式的乘除运算关键是运用二次根式的乘除运算法则.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目