题目内容
【题目】已知直线![]() :
:![]() 与函数
与函数![]() .
.
(1)直线![]() 经过定点
经过定点![]() ,直接写出点
,直接写出点![]() 的坐标:_______;
的坐标:_______;
(2)当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象存在唯一的公共点,在图
的图象存在唯一的公共点,在图![]() 中画出
中画出![]() 的函数图象并直接写出
的函数图象并直接写出![]() 满足的条件;
满足的条件;
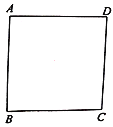
(3)如图![]() ,在平面直角坐标系中存在正方形
,在平面直角坐标系中存在正方形![]() ,已知
,已知![]() 、
、![]() .请认真思考函数
.请认真思考函数![]() 的图象的特征,解决下列问题:
的图象的特征,解决下列问题:
①当![]() 时,请直接写出函数
时,请直接写出函数![]() 的图象与正方形
的图象与正方形![]() 的边的交点坐标:_______;
的边的交点坐标:_______;
②设正方形![]() 在函数
在函数![]() 的图象上方的部分的面积为
的图象上方的部分的面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式.
的函数关系式.

【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)①交点坐标为
;(3)①交点坐标为![]() ,②
,②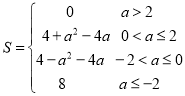 .
.
【解析】
(1)观察可知当x=-2时y=0,所以经过定点![]()
(2)先分类![]() 和
和![]() 讨论
讨论![]() ,分别得y=x,y=2-x,据此画出函数图象,再观察得出k的取值范围.
,分别得y=x,y=2-x,据此画出函数图象,再观察得出k的取值范围.
(3)①当![]() 时,
时,![]() ,画出图象观察即可得出答案.
,画出图象观察即可得出答案.
②分四种情况讨论.设![]() 与正方形交于
与正方形交于![]() 、
、![]() 两点.
两点.![]() 与正方形无交点;
与正方形无交点;![]() 点位于
点位于![]() 边上;
边上;![]() 点位于
点位于![]() 上时;
上时;![]() 点与
点与![]() 点重合.根据四种情况分别画出图形,进行计算.
点重合.根据四种情况分别画出图形,进行计算.
(1)观察可知当x=-2时y=0,所以经过定点![]()
(2)解:![]() 时
时![]() ,图象如图
,图象如图
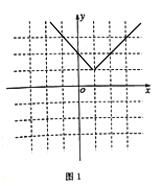
当![]() 或
或![]() 或
或![]() ,直线
,直线![]() 与函数
与函数![]() 的图象存在唯一的公共点,
的图象存在唯一的公共点,
(3)①当![]() 时,
时,![]() ,图象如图.
,图象如图.
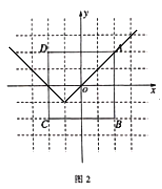
观察可知交点坐标为![]()
②解:由图象可知令顶点为![]()
![]() 与正方形交于
与正方形交于![]() 、
、![]() 两点
两点
1)当![]() 时,
时,![]() 与正方形无交点,如下图所示,此时
与正方形无交点,如下图所示,此时![]() .
.
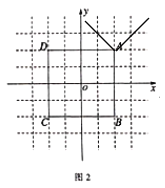
2)当![]() 时,
时,![]() 点位于
点位于![]() 边上
边上
![]()
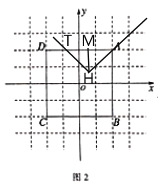
3)当![]() 时,
时,![]() 点位于
点位于![]() 上时
上时

![]()
![]()
4)当![]() 时,
时,![]() 点与
点与![]() 点重合
点重合
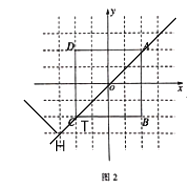
![]()
∴综上所述
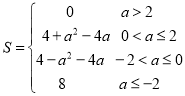

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目