题目内容
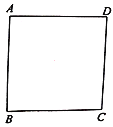
【题目】已知：正方形
，
为平面内任意一点，连接
，将线段绕点
顺时针旋转
得到
，当点
，，
在一条直线时，若
，
，则
________．
【答案】
或
【解析】
分两种情况讨论：
（1）当点G在线段BD上时，如下图连接EG交CD于F；（2）当点G在线段BD的延长线上时，如下图连接EG交CD的延长线于F.根据两种情况分别画出图形，证得
是等腰直角三角形，求出DF=EF=2，然后在直角三角形ECF中利用勾股定理即可求出CE的长.
解：分两种情况讨论：
（1）当点G在线段BD上时，如下图连接EG交CD于F
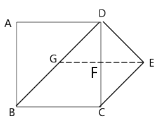
∵ABCD是正方形
∴CD=AD=4
∵线段
绕点
顺时针旋转
得到
∴
是等腰直角三角形，DE=DG= 
∴DF=EF=2
∴CF=CD-DF=4-2=2
∴CE=
（2）当点G在线段BD的延长线上时，如下图连接EG交CD的延长线于F
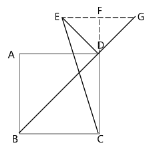
∵ABCD是正方形
∴CD=AD=4
∵线段绕点顺时针旋转得到
∴是等腰直角三角形，DE=DG=
∴DF=EF=2
∴CF=CD+DF=4+2=6
∴CE=
综上所述，CE的长为或
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
