题目内容
如图1，正方形AEFG的顶点E、G分别在正方形ABCD的AB、AD边上，已知
AB=4cm，AG=2cm，把正方形AEFG饶点A顺时针旋转一个角度（如图2），使得G、F、B在同一直线上
（1）求旋转的最小度数，
（2）记EF与AB的交点为H，求AH的长．
解：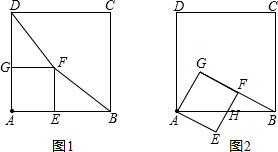
（1）在Rt△ABG中，
∵sin∠ABG=
=
=
，
∴∠ABG=30°，
∴∠BAE=∠ABG=30°，
而∠BAE等于旋转角，
故旋转的最小度数30°；
（2）在Rt△AEH中，
∵∠EAH=30°，AE=2cm，
∴cos∠EAH=
=
=
，
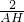∴AH=
．
分析：（1）由于G、F、B在同一直线上，则△ABG为直角三角形，然后利用正弦的定义可求出∠ABG=30°，利用平行线的性质得到∠BAE=∠ABG=30°，再根据旋转的性质得到旋转的最小度数30°；
（2）在Rt△AEH中，由于∠EAH=30°，AE=2cm，利用余弦的定义可计算出AH的长．
点评：本题考查了旋转的性质：旋转前后两图形全等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了正方形的性质以及解直角三角形．
（1）在Rt△ABG中，∵sin∠ABG=
==，∴∠ABG=30°，
∴∠BAE=∠ABG=30°，
而∠BAE等于旋转角，
故旋转的最小度数30°；
（2）在Rt△AEH中，
∵∠EAH=30°，AE=2cm，
∴cos∠EAH=
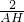==，∴AH=
．分析：（1）由于G、F、B在同一直线上，则△ABG为直角三角形，然后利用正弦的定义可求出∠ABG=30°，利用平行线的性质得到∠BAE=∠ABG=30°，再根据旋转的性质得到旋转的最小度数30°；
（2）在Rt△AEH中，由于∠EAH=30°，AE=2cm，利用余弦的定义可计算出AH的长．
点评：本题考查了旋转的性质：旋转前后两图形全等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了正方形的性质以及解直角三角形．
练习册系列答案
相关题目
22、如图，在正方形ABCD中，E是AB边上任一点，BG⊥CE，垂足为点O，交AC于点F，交AD于点G．（1）证明：BE=AG；
（2）当点E是AB边中点时，试比较∠AEF和∠CEB的大小，并说明理由．
如图，在正方形ABCD，F为DC的中点，E为BC上一点，且EC=
如图，在正方形ABCD中，E是CD的中点，F是BC上一点，且BF=3CF．给出下列结论：①∠DAE=30°；②△ADE∽△AEF；③AE⊥EF；④△ABF∽△ECF．其中正确的个数为（ ）
如图，在正方形ABCD内，作等边三角形BCE，连接AE、DE，并延长DE交AB于F
如图，在正方形ABCD中，E是DC边上一点，△ADE经顺时针旋转后与△ABF重合．