Question

【题目】已知：内接于，为劣弧的中点，．

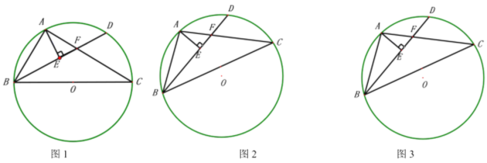
（1）如图1，当为的直径时，求证：；

（2）如图2，当不是的直径，且时，求证：；

（3）如图3在（2）的条件下，，，求长．

Answer 1

【答案】（1）见详解；（2）见详解；（3）．

【解析】

（1）由等角的余角相等，得到∠ABD=∠EAC，由为劣弧的中点，则∠ABC=2∠EAC，即可得到答案；

（2）延长AE交BC于点G，先证明△ABE≌△GBE，则AB=GB，AE=GE，∠BAE=∠BGE，由三角形的外角性质和等量代换，得到CG=AG=2AE，即可得到答案；

（3）延长AE到G，过点D作DH⊥BC，连接DC，OD，由相似三角形的判定和性质，求出所需的边长的长度，结合解直角三角形和勾股定理，即可得到答案．

解：（1）如图1，

∵为的直径，

∴∠BAC=90°，

∵，

∴∠AEF=90°，

∴∠ABD+∠AFB=∠AFB+∠CAE=90°，

∴∠ABD=∠CAE，

∵为劣弧的中点，

∴∠ABC=2∠ABD=2∠CAE，

∵∠ABC+∠C=90°，

∴；

（2）如图，延长AE交BC于点G，

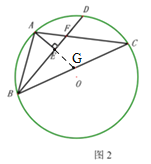
∵AE⊥BD，

∴∠AEB=∠GEB=90°，

∵点D是为劣弧的中点，

∴∠ABE=∠GBE，

∵BE=BE，

∴△ABE≌△GBE（ASA），

∴AB=GB，AE=GE，∠BAE=∠BGE，

∴AG=2AE，

∵，

∴∠BGE=2∠C，

∵∠BGE=∠C+∠CAG，

∴∠C=∠CAG，

∴CG=AG=2AE，

∵BC=BG+CG，

∴；

（3）如图，延长AE到G，过点D作DH⊥BC，连接DC，OD，

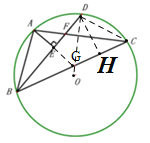
由（2）知，AG=CG，点D为弧AC的中点，

∴点O、G、D三点共线，

∵∠ABE=∠DBH，∠AEB=∠DHB=90°，

∴△ABE∽△DBH，

∴，

∵，，

∴，，

∵DG平分∠AGC，

∴GE=GH，

设，则，

∴，

在Rt△BEG中，，

∴，

∴，

∴，，

∴，

∴，

∴，

∴，

∴，

易证△AFB∽DFC，

∴，

∴．