ĖâÄŋÄÚČÝ
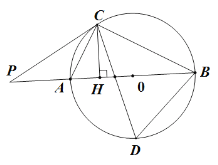
ĄūĖâÄŋĄŋÎŌđúđÅīúĘýŅ§ÖøŨũ(ūÅÕÂËãĘõ)ÖÐÓÐČįÏÂÎĘĖâĢšĄ°―ņÓÐČËģÖ―ðģöÎåđØĢŽĮ°đØķþķøË°ŌŧĢŪīÎđØČýķøË°ŌŧĢŽīÎđØËÄķøË°ŌŧĢŽīÎđØÎåķøË°ŌŧĢŽīÎđØÁųķøË°ŌŧĢŽēĒÎåđØËųË°ĢŽĘĘÖØŌŧ―ïĢŪĄąÆäŌâ˞ΊĄ°―ņÓÐČËģÖ―ðģöÎåđØĢŽĩÚ![]() đØËųĘÕË°―ðΊģÖ―ðĩÄ
đØËųĘÕË°―ðΊģÖ―ðĩÄ![]() ĢŽĩÚ
ĢŽĩÚ![]() đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ
đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ![]() ĢŽĩÚ
ĢŽĩÚ![]() đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ
đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ![]() ĢŽĩÚ
ĢŽĩÚ![]() đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ
đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ![]() ĢŽĩÚ
ĢŽĩÚ![]() đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ
đØËųĘÕË°―ðΊĘĢÓā―ðĩÄ![]() ĢŽ
ĢŽ![]() đØËųĘÕË°―ðÖŪšÍĢŽĮĄšÃÖØ
đØËųĘÕË°―ðÖŪšÍĢŽĮĄšÃÖØ![]() ―ïĢŪĄąČôÉčÕâļöČËÔąūģÖ―ð
―ïĢŪĄąČôÉčÕâļöČËÔąūģÖ―ð![]() ―ïĢŽļųūÝĖâŌâŋÉÁз―ģĖΊ__________ ĢŪ
―ïĢŽļųūÝĖâŌâŋÉÁз―ģĖΊ__________ ĢŪ
Ąūīð°ļĄŋ![]()
Ąū―âÎöĄŋ
ÉčĩÚŌŧđØĘÕË°―ð![]() xĢŽÔōĩÚķþđØĘÕË°―ð
xĢŽÔōĩÚķþđØĘÕË°―ð![]() (1
(1![]() )xĢ―
)xĢ―![]() xĢŽĩÚČýđØĘÕË°―ð
xĢŽĩÚČýđØĘÕË°―ð![]() (1
(1![]()
![]() )=
)=![]() xĢŽĩÚËÄđØĘÕË°―ð
xĢŽĩÚËÄđØĘÕË°―ð![]() (1
(1![]()
![]()
![]() )x=
)x=![]() xĢŽĩÚÎåđØĘÕË°―ð
xĢŽĩÚÎåđØĘÕË°―ð![]() ĢĻ1-
ĢĻ1-![]()
![]()
![]()
![]() ĢĐx=
ĢĐx=![]() xĢŽÓÉīËÁÐģö·―ģĖĢŪ
xĢŽÓÉīËÁÐģö·―ģĖĢŪ
―âĢšÉčĩÚŌŧđØĘÕË°―ð![]() xĢŽÔōĩÚķþđØĘÕË°―ð
xĢŽÔōĩÚķþđØĘÕË°―ð![]() (1
(1![]() )xĢ―
)xĢ―![]() xĢŽĩÚČýđØĘÕË°―ð
xĢŽĩÚČýđØĘÕË°―ð![]() (1
(1![]()
![]() )=
)=![]() xĢŽĩÚËÄđØĘÕË°―ð
xĢŽĩÚËÄđØĘÕË°―ð![]() (1
(1![]()
![]()
![]() )x=
)x=![]() xĢŽĩÚÎåđØĘÕË°―ð
xĢŽĩÚÎåđØĘÕË°―ð![]() ĢĻ1-
ĢĻ1-![]()
![]()
![]()
![]() ĢĐx=
ĢĐx=![]() xĢŽ
xĢŽ
ÓÉĖâŌâŋÉĩÃĢš![]()
đĘīð°ļΊĢš![]() ĢŪ
ĢŪ

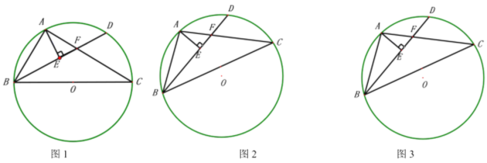
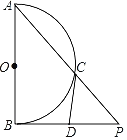
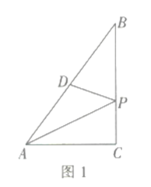
ĄūĖâÄŋĄŋČįÍž1ĢŽÔÚ![]() ÖÐĢŽ
ÖÐĢŽ![]() Ί
Ί![]() ĩÄÖÐĩãĢŽ
ĩÄÖÐĩãĢŽ![]() ĘĮ
ĘĮ![]() ąßÉÏŌŧķŊĩãĢŽÁŽ―Ó
ąßÉÏŌŧķŊĩãĢŽÁŽ―Ó![]() ĢŪČô
ĢŪČô![]() Éč
Éč ![]() (ĩąĩã
(ĩąĩã![]() Óëĩã
Óëĩã![]() ÖØšÏĘąĢŽ
ÖØšÏĘąĢŽ![]() ĩÄÖĩΊ
ĩÄÖĩΊ![]() )ĢŽ
)ĢŽ![]() ĢŪ
ĢŪ
ÐĄÃũļųūÝŅ§Ï°šŊĘýĩÄūŅéĢŽķÔšŊĘý![]() ËæŨÔąäÁŋ
ËæŨÔąäÁŋ![]() ĩÄąäŧŊķøąäŧŊĩÄđæÂÉ―øÐÐÁËĖ―ūŋĢŪ
ĩÄąäŧŊķøąäŧŊĩÄđæÂÉ―øÐÐÁËĖ―ūŋĢŪ
ÏÂÃæĘĮÐĄÃũĩÄĖ―ūŋđýģĖĢŽĮëēđģäÍęÕûĢŪ
![]() ÍĻđýČĄĩãĄĒŧÍžĄĒžÆËãĢŽĩÃĩ―ÁË
ÍĻđýČĄĩãĄĒŧÍžĄĒžÆËãĢŽĩÃĩ―ÁË![]() Óë
Óë![]() ĩÄžļŨéÖĩĢŽČįÏÂąíĢš
ĩÄžļŨéÖĩĢŽČįÏÂąíĢš
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ËĩÃũĢšēđČŦąíļņĘąĢŽÏāđØĘýÖĩąĢÁôŌŧÎŧÐĄĘýĢŪ
(ēÎŋžĘýūÝĢš![]() ) ĢŪ
) ĢŪ
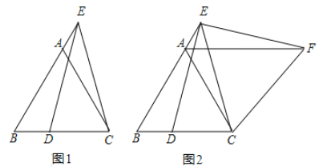
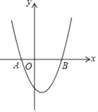
![]() ČįÍž2ĢŽÃčģöĘĢÓāĩÄĩãĢŽēĒÓÃđâŧŽĩÄĮúÏßŧģöļÚŊĘýĩÄÍžÏóĢŪ
ČįÍž2ĢŽÃčģöĘĢÓāĩÄĩãĢŽēĒÓÃđâŧŽĩÄĮúÏßŧģöļÚŊĘýĩÄÍžÏóĢŪ
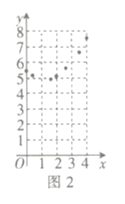
![]() đÛēėÍžÏóĢŽÏÂÁÐ―áÂÛÕýČ·ĩÄÓÐ _ ĢŪ
đÛēėÍžÏóĢŽÏÂÁÐ―áÂÛÕýČ·ĩÄÓÐ _ ĢŪ
ĒŲšŊĘýÓÐŨîÐĄÖĩĢŽÃŧÓÐŨîīóÖĩ
ĒÚšŊĘýÓÐŨîÐĄÖĩĢŽŌēÓÐŨîīóÖĩ
ĒÛĩą![]() ĘąĢŽ
ĘąĢŽ![]() ËæŨÅ
ËæŨÅ![]() ĩÄÔöīóķøÔöīó
ĩÄÔöīóķøÔöīó
ĒÜĩą![]() ĘąĢŽ
ĘąĢŽ![]() ËæŨÅ
ËæŨÅ![]() ĩÄÔöīóķøžõÐĄ
ĩÄÔöīóķøžõÐĄ