题目内容
11．
如图，一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，则函数y=ax2+（b-1）x+c的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 由一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，得出方程ax2+（b-1）x+c=0有两个不相等的根，进而得出函数y=ax2+（b-1）x+c与x轴有两个交点，根据方程根与系数的关系得出函数y=ax2+（b-1）x+c的对称轴x=-$\frac{b-1}{2a}$＞0，即可进行判断．
解答 解：∵一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，
∴方程ax2+（b-1）x+c=0有两个不相等的根，
∴函数y=ax2+（b-1）x+c与x轴有两个交点，
又∵-$\frac{b}{2a}$＞0，a＞0
∴-$\frac{b-1}{2a}$=-$\frac{b}{2a}$+$\frac{1}{2a}$＞0
∴函数y=ax2+（b-1）x+c的对称轴x=-$\frac{b-1}{2a}$＞0，
∴A符合条件，
故选A．
点评 本题考查了二次函数的图象，直线和抛物线的交点，交点坐标和方程的关系以及方程和二次函数的关系等，熟练掌握二次函数的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在⊙O中，AO∥CD，∠1=30°，劣弧AB的长为3300千米，则⊙O的周长用科学记数法表示为3.96×104千米．
如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：
如图，AB是⊙O的直径，AD与⊙O相切于点A，过B点作BC∥OD交⊙O于点C，连接OC、AC，AC交OD于点E．若AB=2，AD=$\sqrt{3}$，则图中阴影部分的面积为$\frac{π}{6}$-$\frac{\sqrt{3}}{4}$．
如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC．若点F是DE的中点，连接AF，则AF=5．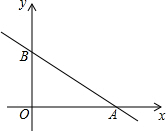
如图，已知直线y=-$\frac{3}{4}$x+3分别与x，y轴交于点A和B．