题目内容
6．李先生乘出租车去某公司办事，下车时，打出的电子收费单为“里程11千米，应收29.10元”．该城市的出租车收费标准如下表所示，请求出起步价N（N＜12）．| 里程（千米） | 0＜x≤3 | 3＜x≤6 | x＞6 |
| 价格 | N元 | $\frac{22}{N}$元/千米 | $\frac{25}{N}$元/千米 |
分析 表格中的含义是：当行车里程不超过3公里时，价格是N元，当行车里程超过了3公里而不超过6公里时，除付10元外，超过的部分每公里再付$\frac{22}{N}$元；若行车里程超过6公里，除了需付以上两项费用外，超过6公里的部分，每公里再付$\frac{25}{N}$元．根据题意列出方程即可求解．
解答 解：依题意，得N+（6-3）×$\frac{22}{N}$+（11-6）×$\frac{25}{N}$=29.10，
整理，得N2-29.1N+191=0，
解得N1=19.1，N2=10．
由于N＜12，所以N=10．
答：起步价是10元．
点评 此题考查了一元二次方程的应用，读懂表格是正确列出方程的基础．找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．
练习册系列答案
相关题目
17．
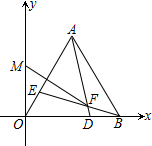如图，在平面直角坐标系中，等边△OAB的边OB在x轴正半轴上，点A（3，m），m＞0，点D、E分别从B、O以相同的速度向O、A运动，连接AD、BE，交点为F，M是y轴上一点，则FM的最小值是（ ）
如图，在平面直角坐标系中，等边△OAB的边OB在x轴正半轴上，点A（3，m），m＞0，点D、E分别从B、O以相同的速度向O、A运动，连接AD、BE，交点为F，M是y轴上一点，则FM的最小值是（ ）| A． | 3 | B． | $\sqrt{3}$+1 | C． | 2$\sqrt{3}$-2 | D． | 6-2$\sqrt{3}$ |
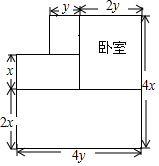如图，是张老师买的经济适用房平面结构示意图，图中标明了有关尺寸（墙体厚度忽略不计，单位：m），房主计划把卧室以外的地面都铺上地砖，
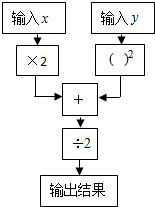求代数式的值：