题目内容
19.已知y=$\sqrt{x-1}$+$\sqrt{1-x}$+$\frac{1}{2}$,则|1-2y|+$\sqrt{{y}^{2}-2y+1}$等于$\frac{1}{2}$.分析 直接利用二次根式有意义的条件得出x,y的值,进而利用绝对值以及二次根式的性质化简求出答案.
解答 解:∵y=$\sqrt{x-1}$+$\sqrt{1-x}$+$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{x-1≥0}\\{1-x≥0}\end{array}\right.$,
解得:x=1,
故y=$\frac{1}{2}$,
∴|1-2y|+$\sqrt{{y}^{2}-2y+1}$
=1-2y+(1-y)
=0+1-$\frac{1}{2}$
=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了二次根式有意义的条件,正确得出x,y的值是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.方程x2-22x+2=0的根的情况为( )
| A. | 有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 有两个相等的实数根 |
10.下列各数中,比-2小的数是( )
| A. | -3 | B. | -1 | C. | 1 | D. | 0 |
7. 实数b在数轴上的位置如图所示,则实数b可能的取值为( )
实数b在数轴上的位置如图所示,则实数b可能的取值为( )
 实数b在数轴上的位置如图所示,则实数b可能的取值为( )
实数b在数轴上的位置如图所示,则实数b可能的取值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{7}$-2 |
8.函数y=$\sqrt{4-3x}$的自变量x的取值范围是( )
| A. | x<4 | B. | x<$\frac{4}{3}$ | C. | x≤4 | D. | x≤$\frac{4}{3}$ |
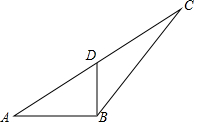 如图,已知△ABC中,中线BD⊥AB,AB=6,BD=4,求tan∠CBD的值.
如图,已知△ABC中,中线BD⊥AB,AB=6,BD=4,求tan∠CBD的值. 如图,OA,OB是⊙O的半径,C是$\widehat{AB}$的中点,CM⊥OA,CN⊥OB,垂足为M,N,求证:AM=BN.
如图,OA,OB是⊙O的半径,C是$\widehat{AB}$的中点,CM⊥OA,CN⊥OB,垂足为M,N,求证:AM=BN. 如图,在矩形ABCD中,AB=6,AD=3,点P是边AD上的一点,联结BP,将△ABP沿着BP所在直线翻折得到△EBP,点A落在点E处,边BE与边CD相交于点G,如果CG=2DG,那么DP的长是1.
如图,在矩形ABCD中,AB=6,AD=3,点P是边AD上的一点,联结BP,将△ABP沿着BP所在直线翻折得到△EBP,点A落在点E处,边BE与边CD相交于点G,如果CG=2DG,那么DP的长是1.