题目内容
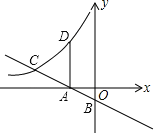
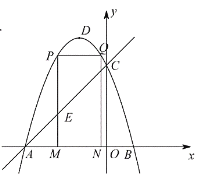
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为![]() ,点C的坐标为
,点C的坐标为![]() .
.
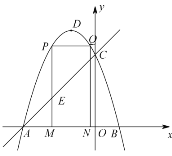
(Ⅰ)求抛物线的解析式;
(Ⅱ)点M为线段![]() 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线
上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线![]() 交于点E,与抛物线交于点P,过点P作
交于点E,与抛物线交于点P,过点P作![]() 交抛物线于点Q,过点Q作
交抛物线于点Q,过点Q作![]() 轴于点N.若点P在点Q左边,当矩形
轴于点N.若点P在点Q左边,当矩形![]() 的周长最大时,求
的周长最大时,求![]() 的面积;
的面积;
(Ⅲ)在(Ⅱ)的条件下,当矩形![]() 的周长最大时,连接
的周长最大时,连接![]() ,过抛物线上一点F作y轴的平行线,与直线
,过抛物线上一点F作y轴的平行线,与直线![]() 交于点G(点G在点F的上方).若
交于点G(点G在点F的上方).若![]() ,求点F的坐标.
,求点F的坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]()
【解析】
(Ⅰ)将点A,点C坐标代入解析式可求解;
(Ⅱ)设M(x,0),P(x,-x2-2x+3),利用对称性可求点Q(-2-x,-x2-2x+3),可求MP=-x2-2x+3,PQ=-2-x-x=-2-2x,则可用x表示矩形PMNQ的周长,由二次函数的性质可求当矩形PMNQ的周长最大时,点P的坐标,即可求点E,点M的坐标,由三角形面积公式可求解;
(Ⅲ)先求出点D坐标,即可求DQ=![]() ,可得FG=4,设F (m,-m2-2m+3),则G (m,m+3),用含有m的式子表示FG的长度即可求解.
,可得FG=4,设F (m,-m2-2m+3),则G (m,m+3),用含有m的式子表示FG的长度即可求解.
解:(Ⅰ)依题意
解得![]()
所以![]()
(Ⅱ)![]()
抛物线的对称轴是直线![]()
![]() ,
,![]() ,其中
,其中![]()
∵P、Q关于直线![]() 对称
对称
设Q的横坐标为a
则![]()
∴![]()
∴![]()
∴![]() ,
,![]()
∴周长![]()
当![]() 时,d取最大值,此时,
时,d取最大值,此时,![]()
∴![]()
设直线![]() 的解析式为
的解析式为![]()
则![]() ,解得
,解得![]()
∴设直线![]() 的解析式为
的解析式为![]()
将![]() 代入
代入![]() ,得
,得![]()
∴![]() ,
,
∴![]()
∴![]()
(Ⅲ)由(Ⅱ)知,当矩形![]() 的周长最大时,
的周长最大时,![]() 此时点
此时点![]() ,与点C重合,
,与点C重合,
∴![]()
∵![]()
∴![]()
过D作![]() 轴于K,
轴于K,
则![]() ,
,![]()
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
设![]() ,则
,则![]()
![]()
∴![]() ,解得
,解得![]() ,
,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() .
.
∴![]() 或
或![]()


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目