Question

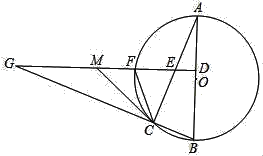
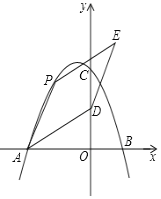
【题目】如图，在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与坐标轴交于A，B，C三点，其中点B的坐标为（1，0），点C的坐标为（0，4）；点D的坐标为（0，2），点P为二次函数图象上的动点．

（1）求二次函数的表达式；

（2）当点P位于第二象限内二次函数的图象上时，连接AD，AP，以AD，AP为邻边作平行四边形APED，设平行四边形APED的面积为S，求S的最大值；

（3）在y轴上是否存在点F，使∠PDF与∠ADO互余？若存在，直接写出点P的横坐标；若不存在，请说明理由．

Answer 1

【答案】(1) y＝﹣x2﹣3x+4；(2)当时，S有最大值；（3）点P的横坐标为﹣2或1或或.

【解析】

（1）将代入，列方程组求出b、c的值即可；

（2）连接PD，作轴交于点G，求出直线的解析式为，设

，则，

，，

当时，S有最大值；

（3）过点P作轴，设，则，

，

根据，列出关于x的方程，解之即可．

解：（1）将、代入，

，

∴二次函数的表达式；

（2）连接，作轴交于点，如图所示．

在中，

令y＝0，得，

∴直线AD的解析式为．

设，则，

，

∴．

，

∴当时，S有最大值．

（3）过点P作轴，设，则，，

，

即

，

当点P在y轴右侧时，，

，或，

（舍去）或（舍去），

当点P在y轴左侧时，x＜0，

，或，

（舍去），或（舍去），

综上所述，存在点F，使与互余点P的横坐标为或或或．