题目内容
13.解方程组:(1)$\left\{\begin{array}{l}{4(x-y-1)=3(1-y)-2}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{3x+3y}{2}=\frac{3x+2y}{5}+2}\\{\frac{3(2x+3y)}{2}=\frac{2(3x+2y)}{3}+\frac{25}{6}}\end{array}\right.$.
分析 (1)方程组整理后,利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{4x-y=5①}\\{3x+2y=12②}\end{array}\right.$,
①×2+②得:11x=22,即x=2,
把x=2代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{9x+11y=20①}\\{6x+19y=25②}\end{array}\right.$,
①×19-②×11得:105x=105,即x=1,
把x=1代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.下列图形属于中心对称图形的是( )
| A. | 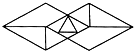 | B. | 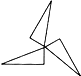 | C. | 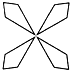 | D. | 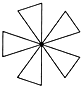 |
 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动