题目内容
【题目】某网店销售单价分别为
元/筒、
元/筒的甲、乙两种羽毛球.根据消费者需求，该网店决定用不超过
元购进甲、乙两种羽毛球共
简.且甲种羽毛球的数量大于乙种羽毛球数量的
.已知甲、乙两种羽毛球的进价分别为
元/筒、
元/筒。若设购进甲种羽毛球
简.
（1）该网店共有几种进货方案?
（2）若所购进羽毛球均可全部售出，求该网店所获利润
（元）与甲种羽毛球进货量（简）之间的函数关系式，并求利润的最大值
【答案】（1）3种；（2）W＝
，最大为1390元
【解析】
（1）设购进甲种羽毛球
筒，根据题意可列出关于m的不等式组，则可求得m的取值范围，再由m为整数即可求得进货方案；
（2）用m表示出W，可得到W关于m的一次函数，再利用一次函数的性质即可求得答案.
解：（1）设购进甲种羽毛球筒，则乙种羽毛球（
）筒，
由题意，得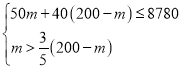
，
解得
.
又∵是整数，
∴m=76，77，78共三种进货方案.
（2）由题意知，甲利润：
元/筒，乙利润：
元/筒，
∴
∵
随增大而增大
∴当
时，
（元）.
即利润的最大值是1390元.
练习册系列答案
名校课堂系列答案
相关题目
