题目内容
3.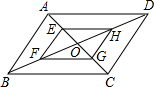 如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.
如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.(1)如果AE=$\frac{1}{2}$AO,BF=$\frac{1}{2}$BO,CG=$\frac{1}{2}$CO,DH=$\frac{1}{2}$DO,那么四边形EFGH是平行四边形吗?证明你的结论;
(2)如果AE=$\frac{1}{3}$AO,BF=$\frac{1}{3}$BO,CG=$\frac{1}{3}$CO,DH=$\frac{1}{3}$DO,那么四边形EFGH是平行四边形吗?证明你的结论;
(3)如果AE=$\frac{1}{n}$AO,BF=$\frac{1}{n}$BO,CG=$\frac{1}{n}$CO,DH=$\frac{1}{n}$DO,其中n为大于1的正整数,那么上述结论还成立吗?
分析 (1)由平行四边形的性质得出OA=OC,OB=OD,再由AE=$\frac{1}{2}$AO,BF=$\frac{1}{2}$BO,CG=$\frac{1}{2}$CO,DH=$\frac{1}{2}$DO,得出OE=OG,OF=OH,根据平行四边形的判定定理即可得出结论;
(2)由平行四边形的性质和已知条件得出OE=OG,OF=OH,即可得出结论;
(3)由平行四边形的性质和已知条件得出OE=OG,OF=OH,即可得出结论.
解答 解:(1)四边形EFGH是平行四边形,理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=$\frac{1}{2}$AO,BF=$\frac{1}{2}$BO,CG=$\frac{1}{2}$CO,DH=$\frac{1}{2}$DO,
∴OE=OG,OF=OH,
∴四边形EFGH是平行四边形;
(2)四边形EFGH是平行四边形,理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=$\frac{1}{3}$AO,BF=$\frac{1}{3}$BO,CG=$\frac{1}{3}$CO,DH=$\frac{1}{3}$DO,
∴OE=OG,OF=OH,
∴四边形EFGH是平行四边形;
(3)上述结论成立;理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=$\frac{1}{n}$AO,BF=$\frac{1}{n}$BO,CG=$\frac{1}{n}$CO,DH=$\frac{1}{n}$DO,
∴OE=OG,OF=OH,
∴四边形EFGH是平行四边形.
点评 本题考查了平行四边形的性质与判定;熟练掌握平行四边形的性质和判定方法是解决问题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
14.要说明“若两个单项式的次数相同,则它们是同类项”是假命题,可以举的反例是( )
| A. | 2ab和3ab | B. | 2a2b和3ab2 | C. | 2ab和2a2b2 | D. | 2a3和-2a3 |
15.下列因式分解正确的是( )
| A. | x2-2x-1=(x-1)2 | B. | 2x2-2=2(x+1)(x-1) | C. | x2y-xy=y(x2-x) | D. | x2-2x+2=(x-1)2+1 |
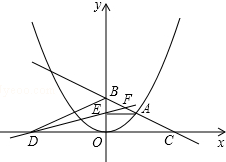 如图,在平面直角坐标系中,A是抛物线y=x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,6),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为a,△BED的面积为S.
如图,在平面直角坐标系中,A是抛物线y=x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,6),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为a,△BED的面积为S.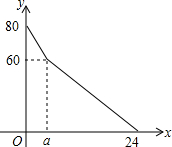 超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.
超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.