题目内容
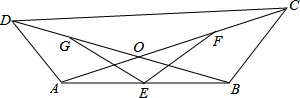 如图,四边形ABCD的对角线AC、BD相交于点O,E、F、G分别是AB、OC、OD的中点,OA=AD,OB=BC,CD=
如图,四边形ABCD的对角线AC、BD相交于点O,E、F、G分别是AB、OC、OD的中点,OA=AD,OB=BC,CD=| 3 |
考点:三角形中位线定理
专题:
分析:连接AG,BF,GF,作EH⊥GF于H,可得GE=FE=
AB,结合三角形中位线定理可得GF=
CD=
AB,在Rt△GHE中利用三角函数可求得∠EGH,从而可得到∠FEG.
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答: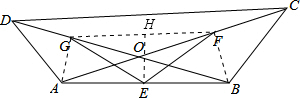 解:连接AG,BF,GF,作EH⊥GF于H,
解:连接AG,BF,GF,作EH⊥GF于H,
∵G、F是OD、OC的中点,
∴GF=
CD=
AB,
∵AO=AD,BO=BC,
∴AG⊥BD,BF⊥AC,
∵E是AB的中点,
∴EG=FG=
AB,
∴GH=HF=
AB,
∴sin∠GEH=∠FEH=
=
,
∴∠GEH=∠FEH=60°,
∴∠FEG=120°,
故答案为:120°.
 解:连接AG,BF,GF,作EH⊥GF于H,
解:连接AG,BF,GF,作EH⊥GF于H,∵G、F是OD、OC的中点,
∴GF=
| 1 |
| 2 |
| ||
| 2 |
∵AO=AD,BO=BC,
∴AG⊥BD,BF⊥AC,
∵E是AB的中点,
∴EG=FG=
| 1 |
| 2 |
∴GH=HF=
| ||
| 4 |
∴sin∠GEH=∠FEH=
| GH |
| EG |
| ||
| 2 |
∴∠GEH=∠FEH=60°,
∴∠FEG=120°,
故答案为:120°.
点评:本题主要考查等腰三角形的判定和性质及三角形中位线定理,通过构造等腰三角形和条件找到GF和AB之间的关系,在Rt△GEF中利用三角函数求得∠EGH和∠EFH是解题的关键.

练习册系列答案
相关题目
已知在△ABC中,∠C=90°,设sinA=m,当∠A是最小的内角时,m的取值范围是( )
A、0<m<
| ||||
B、0<m<
| ||||
C、0<m<
| ||||
D、0<m<
|
 如图,沿AC方向开山修渠,为了加快施工速度,要在小山的另一边同时施工,从AC上的点B取∠ABD=135°,BD=1200米,∠BDE=45°,那么开挖点E离D多远(精确到0.1米),正好能使A、C、E成一条直线.
如图,沿AC方向开山修渠,为了加快施工速度,要在小山的另一边同时施工,从AC上的点B取∠ABD=135°,BD=1200米,∠BDE=45°,那么开挖点E离D多远(精确到0.1米),正好能使A、C、E成一条直线.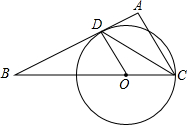 如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C、D两点做⊙O,且圆心O在BC上.
如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C、D两点做⊙O,且圆心O在BC上.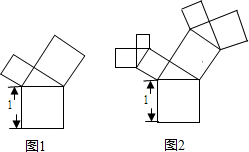 有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( )
有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( ) 如图,四边形ABCD中,AD∥BC,分别以边AB、CD为一边向四边形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N.若EP⊥MN于点P,FQ⊥MN于点Q.判断线段EP、FQ的数量关系,并说明理由.(提示:分别过点A,D作PN的平行线)
如图,四边形ABCD中,AD∥BC,分别以边AB、CD为一边向四边形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N.若EP⊥MN于点P,FQ⊥MN于点Q.判断线段EP、FQ的数量关系,并说明理由.(提示:分别过点A,D作PN的平行线)