题目内容
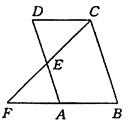
如图，四边形ABCD是平行四边形，点F在BA的延长线上，连接CF交AD于点E．
(1)求证：△CDE∽△FAE．
(2)当E是AD的中点且BC＝2CD时，求证：∠F＝∠BCF．
(1)求证：△CDE∽△FAE．
(2)当E是AD的中点且BC＝2CD时，求证：∠F＝∠BCF．
（1）∵四边形ABCD是平行四边形
∴CD∥AB
∴△CDE∽△FAE；
（2）∵△CDE∽△FAE，DE=EA
∴△CDE≌△FAE
∴CD=AF，
∴BF=2CD
∵BC=2CD
∴BF=BC
∴∠F=∠BCF
∴CD∥AB
∴△CDE∽△FAE；
（2）∵△CDE∽△FAE，DE=EA
∴△CDE≌△FAE
∴CD=AF，
∴BF=2CD
∵BC=2CD
∴BF=BC
∴∠F=∠BCF
此题考查相似三角形的判定及全等三角形的判定的理解及运用
练习册系列答案
活力课时同步练习册系列答案
相关题目
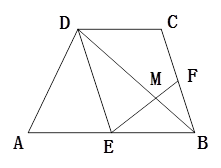
，点E在AC上且
，连结DE并延长它，交BC于点F，交AB的延长线于点G.
时，
的值和
的长；
恰好是
的中点时，求
的长；
的值为多少时，
.请简单说明理由.
，则 △EFD与△ABC的面积比为【 】
B．
C．
D．
为△
的角平分线，
交
于
，如果
，那么
= ．
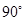，过点C作CD⊥AB于点D，点E为AC上一点，过E点作AC的垂线，交CD的延长线于点F ，与AB交于点G.求证：△ABC∽△FGD
∽
，若
，
，则
的度数是（ ）
