题目内容
若a、b、c满足解:a+b+c=0,abc>0,且 ,y=
,y= ,
,
则x+2y+3xy=________.
2
分析:由a+b+c=0,abc>0,可确定出a、b、c三个数中必有两个为负值,一个为正值
根据绝对值的含义及 可得出x=-1
可得出x=-1
由a+b+c=0与 推出y=3
推出y=3
将x、y代入x+2y+3xy即可求解.
解答:由 a+b+c=0,abc>0可知a、b、c三个数中必有两个为负值,一个为正值,
a+b=-c,a+c=-b,b+c=-a,
∴ =1-1-1=-1,
=1-1-1=-1,
 ,
,
= ,
,
= ,
,
= ,
,
= ,
,
= ,
,
= ,
,
=-3,
则x+2y+3xy=-1+2×(-3)+3×(-1)×(-3)=2,
故答案为2.
点评:本题主要运用a3+b3+c3=3abc(a+b+c=0)这一结论及绝对值的含义来解题.同学们一定弄清y的推导过程.
分析:由a+b+c=0,abc>0,可确定出a、b、c三个数中必有两个为负值,一个为正值
根据绝对值的含义及
 可得出x=-1
可得出x=-1由a+b+c=0与
 推出y=3
推出y=3将x、y代入x+2y+3xy即可求解.
解答:由 a+b+c=0,abc>0可知a、b、c三个数中必有两个为负值,一个为正值,
a+b=-c,a+c=-b,b+c=-a,
∴
 =1-1-1=-1,
=1-1-1=-1, ,
,=
 ,
,=
 ,
,=
 ,
,=
 ,
,=
 ,
,=
 ,
,=-3,
则x+2y+3xy=-1+2×(-3)+3×(-1)×(-3)=2,
故答案为2.
点评:本题主要运用a3+b3+c3=3abc(a+b+c=0)这一结论及绝对值的含义来解题.同学们一定弄清y的推导过程.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.
例:由2x+3y=12,得 ,(x、y为正整数)
,(x、y为正整数)
∴ ,解得0<x<6.
,解得0<x<6.
又 为正整数,则
为正整数,则 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入 .
.
∴2x+3y=12的正整数解为
问题:
(1)请你写出方程2x+y=5的一组正整数解: ;
(2)若 为自然数,则满足条件的x值有 个;
为自然数,则满足条件的x值有 个;
| A.2 | B.3 | C.4 | D.5 |
 ,(x、y为正整数)
,(x、y为正整数) ,解得0<x<6.
,解得0<x<6. 为正整数,则
为正整数,则 为正整数.
为正整数. .
.
 为自然数,则满足条件的x值有 个;
为自然数,则满足条件的x值有 个; 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由 ,(
,(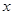 、
、 为正整数)
为正整数)  则有
则有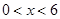 .
. 为正整数,则
为正整数,则 为正整数.
为正整数. ,代入
,代入 .
. 的正整数解为
的正整数解为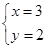
 的一组正整数解:
的一组正整数解:
 为自然数,则满足条件的
为自然数,则满足条件的